第2章 パーセプトロン
![]()
![]()
| 1.1 パーセプトロンの研究の歴史 |
| 1.2 単純パーセプトロン |
| 1.3 多層パーセプトロンの応用 |
| 1.4 ループ構造のある多層パーセプトロン |
| References |
この頁は、平成28年7月7日に新たに開設しました。
この頁は、令和2年5月18日に一部更新しました。
![]()
1.1 パーセプトロンの研究の歴史
ここでは、浅川 (2002)、甘利・外山編 (2000)、Kandel et al. (2013)、Wikipedia (2016)
などを参考にして、パーセプトロンの歴史、
単純パーセプトロン、多層パーセプトロン、
ループ構造のある多層パーセプトロンについて簡単に紹介する。
パーセプトロン (perceptron) は、最初心理学者の Rosenblatt (1958) が提案したもので、
外部刺激図形の学習識別装置のモデルである。なお、Wikipedia (2016) には Rosenblatt (1957)
も引用されている。
パーセプトロンモデルとしては、これまでいろいろな形が知られているが、原則的には外部刺 激図形に対する1)感覚層 (sensory layer)あるいは 入力層 (input layer)、2) 連合層 (associative layer) あるいは隠れ層 (hidden layer)、 および3)応答層(response layer)あるいは出力層 (output layer) と呼ばれる3層から成る階層型ネットワークが仮定される。図1はその 概略を図示したものである。なお、例えばBlock ら (Block, 1962; Block et al., 1962) は、 連合層を associator layer と表記している。ここで、感覚層から応答層への回路はすべてフィード バックなしと仮定される場合が多く、フィードフォワードネットワーク (feedforward neural network) の特別な場合とみれる。
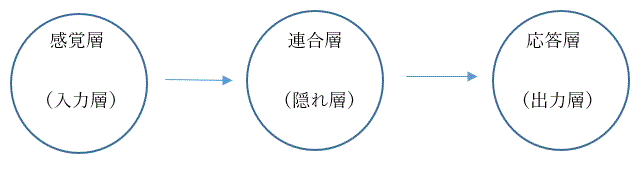
図 1. 一般的な3層パーセプトロンの概略図
ただし、Rosenblatt (1958) の論文では、当初光電パーセプトロン (photo-perceptron) 、すなわち、刺激としての視覚パターンに反応するパーセプトロンが考察さ れており、一部にフィードバックループも含まれている。図1は、Rosenblatt (1958) の Fig.1 に 近いものを描いたものである。これは、一種の4層パーセプトロン (a four-layer perceptron) と見ることができよう。
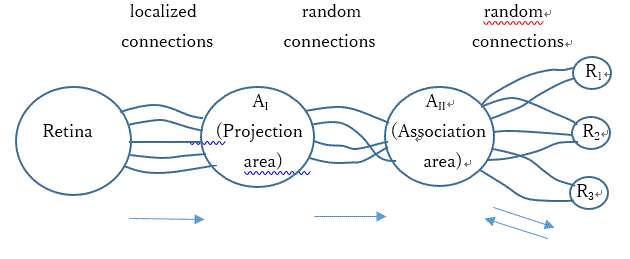
図 2. Rosenblatt (1958) の光電パーセプトロン
図1で、刺激が複数の感覚ユニットあるいは感覚素子 (sensory units,
あるいは S-units)
から成る網膜 (retina) に達すると、1-0型あるいは、刺激強度に比例する振幅もしくは周波数を
持つ反応が得られると仮定する。つぎにそこで得られる反応としてのインパルスは左から2つめの
投影領域(AI)の中の連合細胞 (association cells)
(連合ユニットあるいは連合素子 (A-units))
集合へと伝達される。この投影領域は、幾つかのモデルでは省略され、網膜は直接つぎの連合領域
(association area)(AII)へとつなげられる。また、左から2つめの投影領域と連合
領域間のつながりはランダムであると仮定する。
注意すべきは、図1で AII までの結合は前向き (forward) であるが、最後の結合の段階
、すなわち AII と R-ユニット (R-units) あるいは R-素子
(応答ユニットまたは応答素子 (response units))間の結合は双方向で
ある点である。すなわち、これらの間の結合は、フィードバック結合 (feedback connection) となっ
ている。
パーセプトロンモデルの中で最も単純なネットワークとしては、上記の原則的な3層のうち感覚層と 応答層のみからなるもので、単純パーセプトロンと呼ばれる。次節で見るように、単純パーセプトロン でさえ、その学習規則からはいつも最終解が得られるとは限らず、いわゆる線形 分離可能性 (linear separability) の問題が存在する(例えば、Block, 1962; Duda & Hart, 1973; Minsky & Papert, 1969; Novikoff, A. B. J., 1962; Obradovic & Parberry, 1994)。
一方、入力層と出力層の間の連合層として1つ以上の隠れ層 (hidden-layers) を仮定するモデルは、多層パーセプトロン (multilayer perceptron) ある いは、階層型ニューラルネットワーク (multilayer neural network) と呼 ばれる(例えば、Cottrell et al., 1988; Hornik et al., 1989; Minsky & Popart, 1988; Rumelhart et al., 1986a, b)。
Rosenblattの3層ネットワークの中の連合層を除き、感覚層と応答層の2層から成るネットワーク は単純パーセプトロン (single-layer perceptron or simple perceptron) と呼ばれる。図3は、単純パーセプトロンの構造を示す。
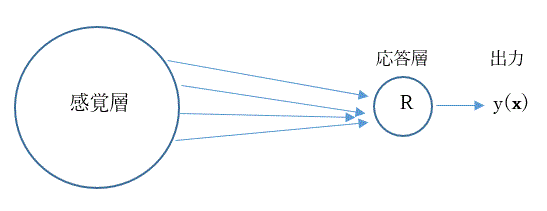
図 3. 単純パーセプトロン
感覚素子 (S-unit) からの出力を x=(x1,x2,…, xn)t (すなわち、列ベクトル)、応答素子 (R-unit) の出力を y(x) とすると、単純パーセプトロンは 次のように書ける:
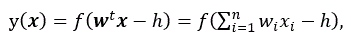
|
(1) |
ここで、y(x) は応答素子の出力を、x は感覚素子の n 個の出力 xi (i=1,2, …, n) を要素とする n 次元ベクトルを、w は xi に対する荷重 wiを要素とする n 次元(列)ベクトルを表す。また、h は閾値 (threshold) であり一般に実数値をとるものとする。また、上式での f(u) は
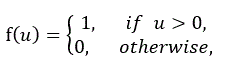
|
(2) |
で定義される階段関数 (step function) である。
(1)式における x および w に対して、x+=
(xt, -1) t および w+=
(wt, h) t を定義すると、次式が成り立つ。
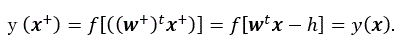
(3)
ここで、単純パーセプトロンの学習目標は、学習したい信号の集合に属するとき1を属さないい とき0を出力するような荷重ベクトル w および閾値 h の組を見出すことである。この時 z(x+) をパーセプトロンが学習すべき望ましい出力とすると、われわれは w+=(wt, h) t を次式のように更新すればよい:
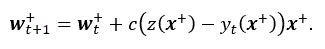
|
(4) |
ここで、c は正の定数である。このような学習ルール (learing rule) は、いわば外部の教師から出力の正誤の情報を得て進められるので、教師あり 学習 (supervised learning) の一種といえる。
これに対して、ヘブ則のような教師なし学習 (unsupervised learning) ルールを用いると、ネットワークは誤りシグナルなしに感覚入力から学習するこ とができる。
多層パーセプトロンは、Rumelhart et al. (1986a, 1986b) により提唱されたモデルで、 甘利・外山(2000)によれば多層パーセプトロンは階層型ニューラルネットワークとも 呼ばれ、ニューロンをそのシナプスの部分まで込めて単純化したモデルであるユニット (unit) なる情報処理素子を一方向にのみ情報が流れるように結合したフィードフォワード ニューラルネットワークモデルである。
なお、ここでのユニットの構造は前節の単純パーセプトロンと同一であるが、出力 y(x) を構成する関数 f は(2)式のような 1-0 型ではなく、次式であらわされる シグモイド関数 (sigmoid function) などの有界な単調増加関 数が用いられる。
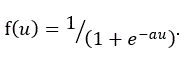
|
(5) |
ここで、(5)式における a はゲイン (gain) と呼ばれる。a=1 の場合のシグモイド関数は、標準シグモイド関数 (standard sigmoid function) と呼ばれる。図4は、標準シグモイド関数を示す。
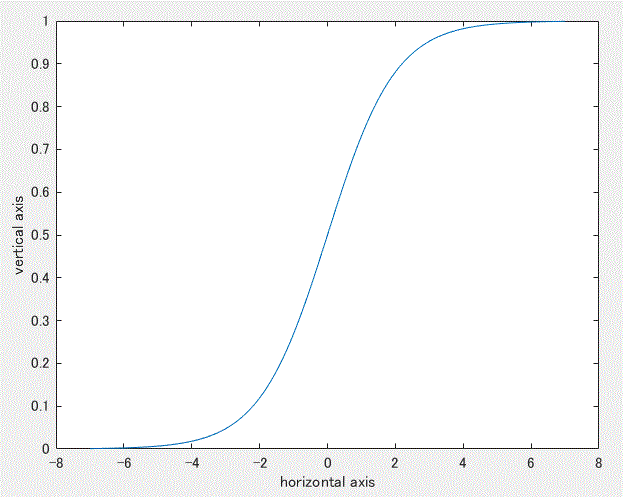
図 4. 標準シグモイド関数
この関数は横軸の値 u が無限大の時1となり、u がマイナス無限大の時0となる連続関数で ある。なお、y=1 および y=0 が漸近線である。
図5は、多層パーセプトロンの1つの例として、3層パーセプトロンの例示したものである。
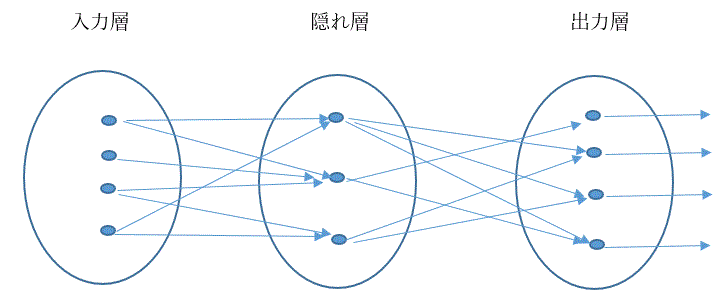
図 5. 3層パーセプトロンの例
なお、多層パーセプトロンの出力関数の近似に関する定理が 1980 年代の後半から提案 されている(Cybenko, 1989; Hornik, 1989, 1991; Funahashi, 1989; Ito, 1989)。
1. 4 ループ構造のある多層パーセプトロン
前節までに述べたパーセプトロンは、原則としてフィードフォワードニューラルネットワーク
であったが、その後それにループ(回帰)構造を追加したフィードバックニューラルネットワー
クも提案されている(Jordan, 1986; 松葉、1995)。
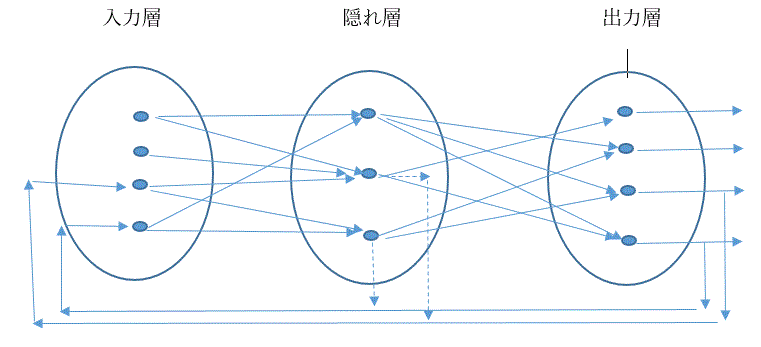
図 6. ループ構造のある多層パーセプトロン
甘利俊一・外山敬介 (2000). 脳科学大事典 朝倉書店
Block, H. D. (1962). The perceptron: A model for brain functioning. I*. Reviews of Modern Physics, 34, 123-135.
Block, H. D., Kight, JR., B. W., & Rosenblatt, F. (1962). Analysis of a four-layer series-coupled perceptron. II*. Reviews of Modern Physics, 34, 135-142.
Kandel, E. R., Schwartz, J. H., Jessell, T. M., Siegelbaum, S. A., & Judspeth, A. J. (2013). Principles of Neural Science, 5th edition. New York: McGraw-Hill.
Rosenblatt, F. (1957). The Perceptron--a perceiving and recognizing automaton. Report 85-461-1, Cornel Aeronautical Laboratory.
Rosenblatt, F. (1958). The perceptron: a probabilistic model for information storage and organization in the brain. Psychological Review, 65, 386-408.
Rumelhart, D. E., Hinton, G. E., & Williams, R. J. (1986a). Learning representations by back-propagating errors. Nature, 323, 533-536.
Rumelhart, D. E., Hinton, G. E., & Williams, R. J. (1986b). Learning internal representations by error propagation. In D. E. Rumelhart, J. L. McClelland and the PDP Research Group, eds., Parallel Distributed Processing, Vol.1, pp.318-362. MIT Press.
Wikipedia (2016). https://en.wikipedia.org/wiki/Perceptron