第3章 リカレントニューラルネットワーク
![]()
![]()
| 3.1 リカレントニューラルネットワークの研究の歴史 |
| 3.2 非自励系を用いたリカレントニューラルネットワーク |
| 3.3 対称結合回路の非自励系による表現 |
| References |
この頁は、平成28年7月17日に新たに開設しました。
この頁は、令和2年5月18日に一部更新しました。
![]()
3.1 リカレントニューラルネットワークの研究の歴史
リカレントニューラルネットワーク (recurrent neural networks)(以降、
RNN と略す)は再帰型ニューラルネットワーク、あるいは
回帰結合回路(甘利・外山、2000)と呼ばれるフィードバックルー
プ(結合)を持つ神経回路網をさす。甘利・外山によれば、RNN は一般の
力学系 (dynamical system) を近似できるという。
一般に力学系では系の状態を n 次元状態空間 (state space) 上の列ベクトル x=(x1, x2, …, xn)t で表すとして、自励系(あるいは 自律系)(autonomous system) ならば、(1) 式で表される:
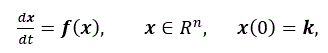
|
(1) |
一方、非自励系 (nonautonomous system) ならば、(2) 式で表さ れる:
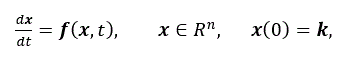
|
(2) |
RNN の文脈では、通常 (2) 式の非自励系(非自律系)として、外部入力 s を仮定した 力学系を考える。ただし、ここでは、x も s も共に時間の関数であることを明記 して、(3) 式のように書くものとする:
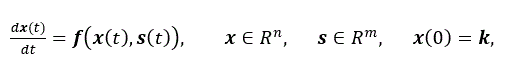
|
(3) |
Sato and Murakami (1991) によれば、(3) 式の力学系を RNN で近似すると次式と書ける:
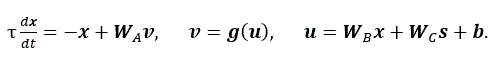
|
(4) |
ここで、g は k 次元列ベクトル u の各要素にシグモイド関数を施すベクトル関数、 k 次元列ベクトル v はシグモイド素子の出力、u はシグモイド素子の入力、n 次元 列ベクトル x はシグモイド素子からの入力を時定数τで時間積分して出力する動的素子の 出力と見れる。一方、k 行 n 列行列 WB は動的素子からシグモイド素子への結合 係数を要素とする行列、k 行 m 列行列WC は外部出力 s からシグモイド素子 への結合係数を要素とする行列、n 行 k 列行列 WA はシグモイド素子から動的 素子への結合係数を要素とする行列である。また、b はシグモイド素子へのバイアス入力で ある。
甘利俊一・外山敬介 (2000). 脳科学大事典 朝倉書店
Sato, M. (1990). A learning algorithm to teach spatiotempral patterns to recurrent neural networks. Biological Cybernetics, 62, 259-263.
Sato, M., & Murakami, Y. (1991). Learning nonlinear dynamics by recurrent neural networks. Proceedings of Symposium on some problems on the theory of dynamical systems in applied science, pp.49-63. World Scientific.