この頁は、令和2年5月6日に一部修正しました。
A 大学心理学科100名に対して、政府の消費税5パーセントアップの政策に対す る態度をガットマン尺度により測定し分析するため、30項目の態度項目を用いて 調査を行ったとする。このような測定により得られる各個人の態度得点がつぎのようで あったとする:
|
当日の問題の標本数 N は100である。
大標本のデータから、度数分布表を作成し、度数分布表を用いての中央値と 四分領域等を求める
上の例でのデータは、名義、順序、間隔、比率の4つの尺度レベルのいずれに該当する か
手計算で、大標本のデータから 第1四分位数 (the first quartile) 、 中央値 (median、略して Mdn)、 第3四分位数 (the third quartile) 、及び、 四分領域 (semi-interquartile range) を求める
中央値とは、データを小さい順に並べた時、ちょうど中央(50パーセント)にくる 値で、メディアンとも呼ばれる。また、四分領域とは、
| Q = ( Q 3 - Q 1 ) / 2 |
として定義される。ここで、Q 1 はデータの小さい順から25パーセント目に位置 する値で第1四分位数と呼ばれる。同様に、Q 3 はデータの小さい順から75パーセ ント目に位置する値である。
以下に、Q 1 、Mdn 、及び Q 3 の公式を示す。これらは、データを比例配分することにより容易に得られる:
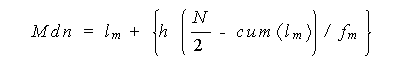
|
(4.1) |
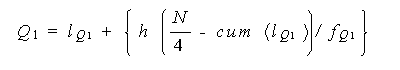
|
(4.2) |
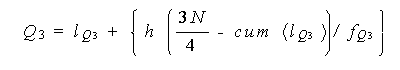
|
(4.3) |
ここで、l m 、l Q 1 、及び l Q 3 は、それぞれ中央値、第1四分位数、 及び第3四分位数のある階級の下限点である。
また、f m 、 f Q 1 、及び f Q3 は、それぞれ中央値、第1四分位数、 及び第3四分位数のある階級の度数である。
また、cum ( l m )、cum( l Q 1 )、及び cum ( l Q 3 ) は、それぞれ中央値、第1四分位数、及び第3四分位数のある階級より1つ手前までの階級の累積 度数である。
最後に、h は階級の幅、N は標本数である。
- 1. 度数分布表について
- 岩原(著)教育と心理のための推計学/ 第3章
- 2. 中央値について
- 岩原(著)教育と心理のための推計学/ 第4章 4.3 節 中央値
- 3. 四分領域について
- 岩原(著)教育と心理のための推計学/ 第5章 5.3 節 四分領域