| 7.1データ |
| 7.2目的 |
| 7.3注意事項 |
| 7.4問題 |
| 7.5予習課題と予習箇所 |
| 7.62×2 分割表の場合のカイ2乗検定の計算手順 |
| 7.7カイ2乗検定量とそれによる検定公式 |
| 7.8実習レポートの記入の仕方 |
| 7.9 統計ソフト SAS を用いたクロス表のカイ2乗値の計算及び検定の実行手順 |
このページは、平成14年6月1日に開設しました。
このページは、令和2年5月6日に一部更新しました
この章では、2組の定性的変数間の関連の強さの有無を統計的に検討するための 1つの方法としての カイ2乗検定 (chi-square test) を学ぶ。
教育や心理の分野では、しばしば被験者は多くのアンケート項目や検査項目に回答
したり、複数の実験条件に対して反復測定を受ける。このような場合、測定値間には
一般にある種の関連が生じる。測定値がすべて名義尺度のレベルであれば、一方の尺度
のカテゴリーを行に、他方の尺度のカテゴリーを列にとり、対応するセルの度数を
カウントすれば、下のような クロス表 (cross table) もしくは 分割表
(contingency table) が構成できる。ここで、一般的には行カテゴリー数は r 個、
列カテゴリー数は s 個であるとする。また、被験者総数は N であるとする。さ
らに、各行の合計 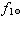 、
、
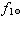 、・・・ や、各列の合計
、・・・ や、各列の合計
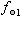 、
、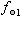 、・・・ などは、 周辺度数 (marginal
frequency) と呼ぶ:
、・・・ などは、 周辺度数 (marginal
frequency) と呼ぶ:

|
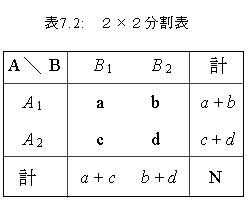
ここでは、2つの名義尺度のカテゴリーが共に2選択肢の場合を例に取り、カイ 2乗検定の手続きを学ぶ。この場合には、分割表はつぎのようになる:
|
例えばデータは、N 人の被験者の性別と向性(外向的、か内向的か)あるとする。 一般的には、それらは以下のように書ける。ここで、G i は被験者 i の性別で 例えば男なら1、女なら2とコード化するものとする。また、E i は同じく被験者 i の向性で、やはり外向的なら1、内向的なら2とコード化したとする:
|
当日の問題の標本数 N は20である。
N 人の被験者の名義2尺度の対データから、2組の定性変数間の関連性の有無を 検討するための1つの方法としてのカイ2乗検定を行う。
なし
卓上計算機を用い、名義2尺度から成る対データから分割表を作成し、さらにカイ 2乗検定により2つの尺度間の関連性の有無の統計的有意性の検定を行え。
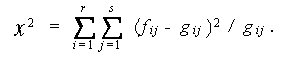
|
(7.1) |
ここで、
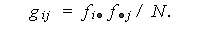
|
(7.2) |
(7.2) 式の g ij は、2つの属性 A 、 B が互いに独立(関連無し)の もとで ( i , j ) セルに期待される度数であり、 期待度数 (expected frequency) と呼ばれている。
また、(7.1) 式から明らかなように、この式の左辺の χ 2 は、各セルに ついての次式で与えられる量 h ij の和、として定義されているので、h ij は、全体的なカイ2乗に対する各セルの寄与の程度を表している。したがって、 帰無仮説が棄却された場合には、上の期待度数とこの量 h ij を同時に出力 できていれば、2つの属性 A 、B のどこにとりわけ大きな独立性からのずれが どの方向にあるのかを検討できることになる。
| h ij = ( f ij - g ij )2 / g ij . | (7.3) |
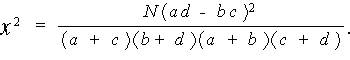
|
(7.4) |
ただし、セル内に期待度数5以下の度数が存在する場合 には、つぎのように イエーツの修正 (Yates' correction in chi square) を行うこと(SAS 方式):
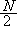 の時、(7.4) 式の分子の ad - bc を
ad - bc -
の時、(7.4) 式の分子の ad - bc を
ad - bc -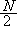 とする。
とする。
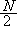 以下の時は、
(7.4) 式のカイ2乗値をゼロとする。
以下の時は、
(7.4) 式のカイ2乗値をゼロとする。
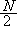 の時、(7.4) 式の分子の ad - bc を
ad - bc +
の時、(7.4) 式の分子の ad - bc を
ad - bc + 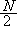 とする。
とする。
上記の (7.1) 式のカイ2乗統計量は、近似的に自由度 ν =( r -1) ( s -1) なる χ 2 - 分布に従う。したがって、通常の方 式により、有意水準に対する棄却点の値を数表から読みとり、標本のカイ2乗統 計量が棄却点の値を超えていれば帰無仮説を棄却、さもなければ採択する。
もちろん、ここでの帰無仮説は、「名義両尺度(変数)間に関連がない」、と いうものである。
これまで、手計算によるクロス表のカイ2乗検定量とその検定の計算方法につ いて述べてきたが、以下の2つの例は、国際的な統計ソフト SAS を用いた クロス表のカイ2乗検定量の計算とその検定の手順を示す。
ここでは、クロス表のカイ2乗検定の計算と検定を行うための SAS プログラム を紹介する。SAS を実行する手順を示す前に、ここで利用するデータと出力結 果の一部、及びそのための SAS プログラムを紹介する。
| 7.9.1.1データ例とその入力方法 |
| 7.9.1.2出力結果の例 |
| 7.9.1.3SAS プログラムの例 |
| 7.9.1.4SAS による具体的手順 |
つぎのデータは、ここでは、心理統計学のテキストの乱数表から取った架空 のデータである。
ここでは、クロス表のカイ2乗検定用に、もとのデータをす べて1か2に各自で変換してから次の例のように入力せよ。変換は、もしデータ が50未満なら1、50以上なら2とせよ。いつもと同様、データは半角で入力 せよ。
1 1 1 2 2 2 3 1 2 4 1 1 5 2 1 6 1 1 7 2 1 8 2 1 9 1 1 10 2 2 11 1 2 12 1 2 13 1 1 14 1 2 15 2 1 16 1 2 17 1 1 18 1 1 19 1 2 20 1 2 |
学生諸君は、心理統計学のテキストの乱数表の中から、各自の通し番号に 対応する箇所から、縦に見て続けて20個を各ページから取り出し、それぞれをすべ て1か2に指定された方法で変換せよ。
ここで、うえの20個のデータの各行は20人の被験者に対応し、各行とも最 初の2桁の数値が被験者番号を、1つ空白を置き1桁で打ってあるのが、p.445 の 各自の学籍番号に対応する20個の値のそれぞれを1か2に変換した値、さらに1 つの空白を置き1桁で打ってあるのが、p.446 の各自の学籍番号に対応する20 個の値をやはりそれぞれを1か2に変換した値、であるとする。もちろん、デ ータはすべて全角ではなく、半角で入力せよ。また、被験者番 号が9番までの被験者の被験者番号は、半角スペースを1つ入れた後一桁の被験者 番号を上の例のように入力すること。
学籍番号に対応する各人のデータの先頭は、各ページごと、左上から右下に向かって 2桁の数値を5つづつ飛ばして到達する位置とする。各列の最後に来たら、次の列の先 頭に戻りカウントすること。
例えば、学籍番号 001 の学生は、p.445 の数値の左最上部の数値から始め、94, 18, ..., 90, 35 までを20名の被験者の第1変数の20個のデータとし、p.446 の数値 の左最上部の数値 70, 99, ..., 95, 45 までの20個のデータを20名の被験者の 第2変数の20個のデータとして、上記データファイルに上の例のように1か2に 変換後の2変数が対になる形に入力する。
また、例えば学籍番号 012 の学生ならば、p.445 の数値左最上部から2列目の6つ目 の数値から始め、81, 18, ..., 29, 38 を第1変数のの20個のデータ、p.446 の数 値の左最上部から2列目の6つ目の数値から始め、96, 62, ..., 29, 61 を第2変数 の20個のデータとして、それぞれを50未満なら1、50以上なら2なる値に変換 したものを入力する。
以下の検定結果は、後続の SAS プログラムよって得られたものである。
a chi-square test for a contingency table
FREQ プロシジャ
表 : catx * caty
catx(categorical variable x)
caty(categorical variable y)
度数 |
期待度数 |
セルのχ 2 乗値|
パーセント |
行のパーセント |
列のパーセント | 1| 2| 合計
---------------+--------+--------+
1 | 7 | 7 | 14
| 7.7 | 6.3 |
| 0.0636 | 0.0778 |
| 35.00 | 35.00 | 70.00
| 50.00 | 50.00 |
| 63.64 | 77.78 |
---------------+--------+--------+
2 | 4 | 2 | 6
| 3.3 | 2.7 |
| 0.1485 | 0.1815 |
| 20.00 | 10.00 | 30.00
| 66.67 | 33.33 |
| 36.36 | 22.22 |
---------------+--------+--------+
合計 11 9 20
55.00 45.00 100.00
catx と caty の統計量
統計量 自由度 値 p 値
----------------------------------------------------------
χ 2 乗値 1 0.4714 0.4924
尤度比χ 2 乗値 1 0.4793 0.4888
連続性補正χ 2 乗値 1 0.0385 0.8445
Mantel-Haenszel のχ 2 乗値 1 0.4478 0.5034
φ係数 -0.1535
不確実性係数 0.1517
Cramer の V 統計量 -0.1535
WARNING: セルの 50% において、期待度数が 5 より小さく
なっています。χ 2 乗検定は妥当な検定で
ないと思われます。
FREQ プロシジャ
catx と caty の統計量
Fisher の正確検定
-----------------------------
セル (1,1) 度数 (F) 7
左側 Pr <= F 0.4257
右側 Pr >= F 0.8808
表の確率 (P) 0.3065
両側 Pr <= P 0.6424
サンプルサイズ = 20
|
うえの出力結果のうち、全体としてのカイ2乗検定結果は、後半の「統計量」の項 に示されている。最初のカイ2乗値は、イエーツの修正をしない場合のカイ2乗値で ある。期待度数に5以下のものがない場合は、この値に対応する p 値により検定を行 う。
一方、いずれかのセルに期待度数5以下のものがある場合は、「統計量」の項の3 つ目のカイ2乗値を見よ。これが、いわゆるイエーツの修正後のカイ2乗 値であることに注意せよ。この場合、検定はもちろんこれに対応する右端の p 値に より行う。
平成28年度からは、つぎの2種類のプログラムの中の最初の SAS 無償バージョン用の プログラムを用いること。
*-----------------------------------------------------------------------*
| February 2, 2016 |
| |
| a sas program for computing the chi-square statistic and testing |
| the null hypothesis about association between two categorical vari- |
| ables. |
*-----------------------------------------------------------------------*;
filename data '/folders/myfolders/data/chisq_ex1.txt';
options ps=60;
data work;
infile data;
input ssno 2. (catx caty) (2.);
label catx="categorical variable x"
caty="categorical variable y";
run;
title 'a chi-square test for a contingency table';
proc freq data=work;
tables catx*caty/expected cellchi2 chisq;
run;
|
*-----------------------------------------------------------------------*
| December 1, 2004 |
| |
| a sas program for computing the chi-square statistic and testing |
| the null hypothesis about association between two categorical vari- |
| ables. |
*-----------------------------------------------------------------------*;
filename data 'p:\data\chisq_ex1.txt';
options ps=60;
data work;
infile data;
input ssno 2. (catx caty) (2.);
label catx="categorical variable x"
caty="categorical variable y";
run;
title 'a chi-square test for a contingency table';
proc freq work;
tables catx*caty/expected cellchi2 chisq;
run;
|
| chisq_ex1.sas |
情報処理教育センター (ecip) で行う場合
![]()