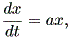
| (1.1) |
この章では、微分力学系の入門レベルの内容について述べる。微分力学系とは、微分 方程式もしくはその組により記述される系をいう。一般に力学系では、系の状態は1 つないしは複数の変数(これは状態変数 (state variable) と呼ばれる)により 記述できるとの仮定に基づき、それら個々の変数の値の瞬間的変化(数学的には、各 変数の時間に対する一次導関数、あるいは微係数)を状態変数の関数として表す。例え ば、状態変数が1つ (例えば x ) で、状態変数の関数が ax という関数だとすれ ば、 (1.1) 式のように表す。
ここで、状態変数が n 個存在するとき、それらにより構成される可能な変数の 組 (x1, x2, . . . , xn) は、系の 状態空間 (state space) と呼ばれ る。状態空間が実数空間(例えばユークリッド空間)であれば、実力学系になる し、複素空間(例えばヒルベルト空間)であれば、複素力学系となる。
状態変数には、いろいろなものが考えられる。例えば、後に見るある化学系では、 状態変数は化学物質の濃度であったり、何らかの物質の分子数であったりする。 また、ある物理系では状態変数は、簡単な電気回路の電流、電圧、抵抗の値であった りする。ある生物系では、状態変数は毎年発生する蝉の数であったり、細胞の神経回路 の膜電位であったりする。
ここでは、各種微分方程式 (differential equation) とその 解曲線 (solution curve) のうち、最も単純なケース
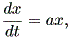
| (1.1) |
について述べる。
この方程式の1つの解 (a solution) は、 k を任意の定数として、
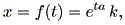
| (1.2) |
と書ける。実は、 (1.1) 式の解は( k を固定すれば)、一意的に定まることを証明 できる。このことから、 (1.1) 式を初期値問題 (an initial value problem) の形、すなわち
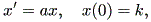
| (1.3) |
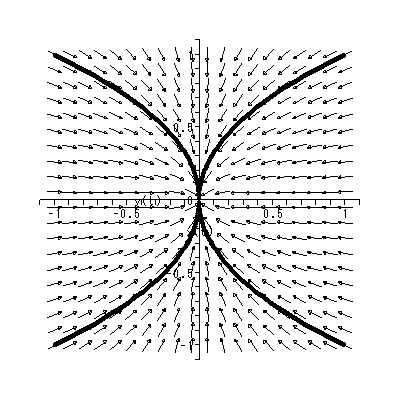
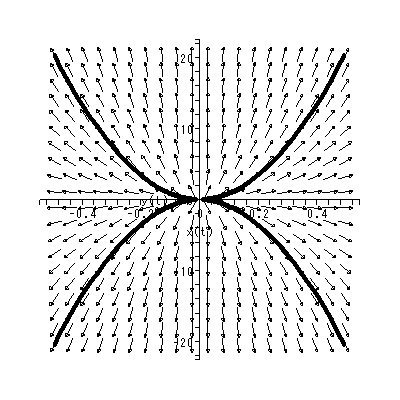
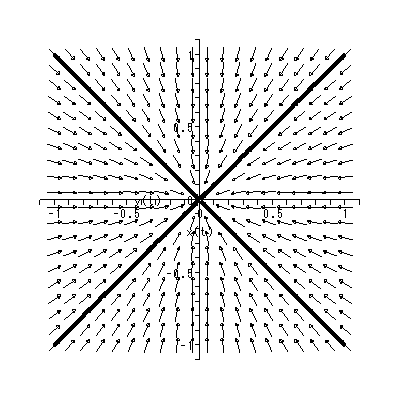
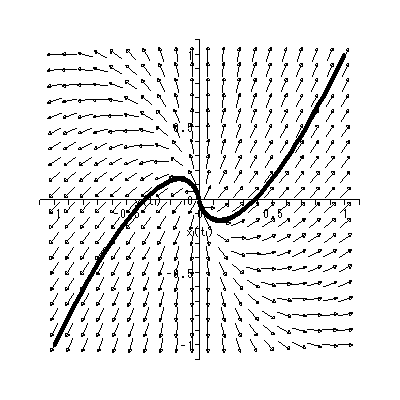
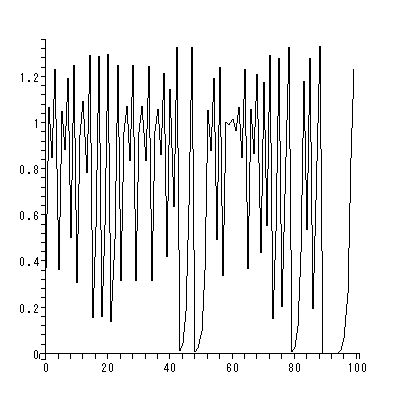
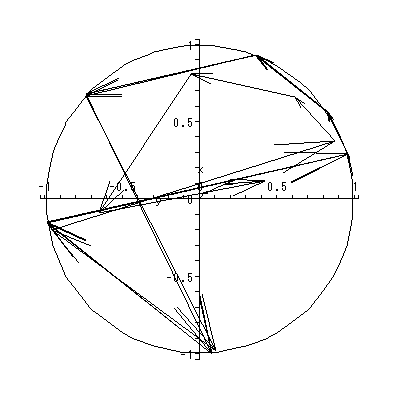
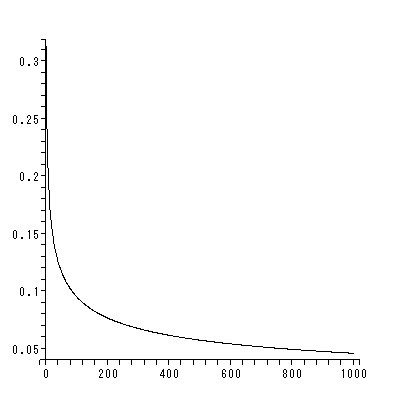
と書くと、 (1.1) 式の場合、その初期値問題は 一意解 (a unique solution) を 持つ、と言える。図 1.1 は、 a = 0.1 の場合、 (1.2) 式の k の値を -2, -1, 1, 2 と変え、解曲線を Maple 9 パッケージにより描かせた結果である。
ただし、一般の微分方程式の場合、その初期値問題に対しては必ずしも一意解は存在 するとは限らず、解の一意性 (uniqueness of solutions) の問題として知られ ている。また、解の存在の有無についても、初期点の近くの点 t で解が存在するか という、局所的存在 (local existence) の問題や、どの範囲の t に対して解 が存在するのかという、大域的存在 (existence in the large) の問題も存在 する。これらの問題については、このテキストの範囲を超えるので省略する。これら の問題については、例えば Hartman (1982) が詳しい。ここでは、Hartman に掲載さ れている1つの例をあげるにとどめる。この例では、初期値問題に対して解は定義域 により2種類存在する:
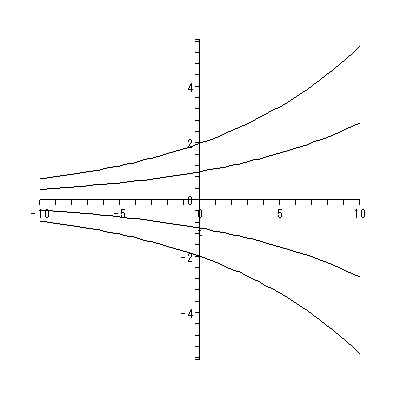
|
[例] 初期値問題
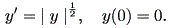
| (1.4) |
は、 c ≧ 0 について、 t ≦ c に対しては、 y (t) = 0 であるが、 t ≧ c では、 y (t) = (t-c)2 / 4 を解として持つ。
[演習 1.1] (1.1) 式の解は、 (1.2) 式以外にないこと(一意性)を証明せよ。
つぎに、 (1.3) 式の解曲線の分類をする。 (1.2) 式から容易につぎの分類ができる:
|
Fig.1 では、 a = 0.1 の場合の、4種の初期値( 図では上から順に k = 2, 1, -1, -2 ) に対する解曲線が描かれているので、うえの分類の第1のケースにあたる。
(註1) (1.1) 式は、線形斉次一階微分方程式 (linear homogeneous first-order differential equations)
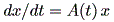
|
の特別なケースである。
(註2) 斉次方程式 (homogeneous equation) とは、 (1.1) 式のよ うに右辺に x に関する定数項がない方程式、非斉次方程式 (nonhomogeneous equation) とは、 (1.1) 式のように右辺に x に関する定数項 B (t) を含む方程式、すなわち
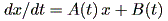
|
なる形の方程式をいう。
(註3) 高階微分方程式 (higher-order differential equations) とは、2次微分以上の項を持つ場合、例えば、
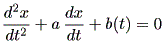
|
などをいう。
状態空間が多次元の場合の線形一次微分方程式の組は、線形一次微分方程 式系 (a system of linear first-order differential equations) と呼ばれ、つ ぎのように書かれる:
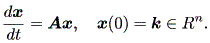
| (1.5) |
(1.5) 式の系の解曲線は、つぎのようになる:
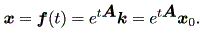
| (1.6) |
(註1) ここで、 etA = ∑k = 0∞ Ak / k ! である (Hirsch & Smale, 1974, p.86).
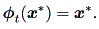
| (1.7) |
そのため、点 x* は 停留点 (a stationary point)、固定点 (a fixed point)、 ゼロ点 (a zero point)、 又は 特異点 (a singular point, or singularity) とも呼ばれる。
(註1) 微分方程式系でも平衡点と固定点(不動点、特異点等)とは区別していること に注意。平衡点は、微係数がゼロになる点であり、一方固定点は解軌道が動かなくなる 点である。
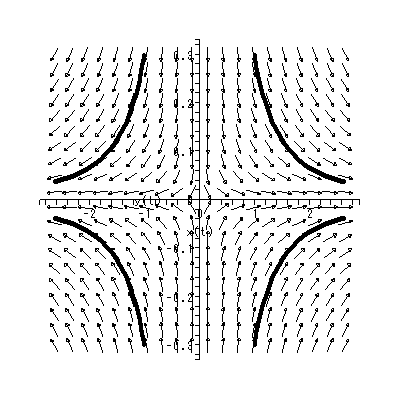
いずれにせよ、特異点の近傍での解曲線の振る舞いは、 (1.5) 式の場合、行列 A の固有値の特徴に依存する。なぜならば、 dx / dt = A x に対して座標変換 x = Py ( P は正則)を施せば、 (1.5) 式は、つぎのように書ける:
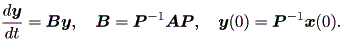
| (1.8) |
[演習 1.2] dx / dt = A x に対して、 (1.8) 式を証明せよ。
ここで、もし P を A の固有ベクトルに取れば、通常の固有値問題とみれ る。ただし、微分方程式の文脈では、一般に A は非対称なので、固有値も固有ベ クトルも一般には複素数から成る。そこで、微分方程式系では、同じく A の相似 変換の1つである実標準形 (real canonical form) を考えることにより、実 (係数)微分方程式系の解を求める
|
|
一般に n 次の実非対称行列 A は、つぎの実標準形の形に書ける:

| (1.9) |
ここで、行列 J1 、 J2 、 ・・・ は、基本(初等)ジョルダン行列 (elementary Jordan matrices) または、基本(初等) λ- ブロック (elementary λ- blocks) と呼ばれ、
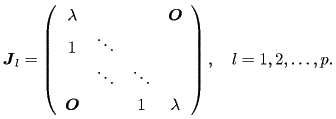
| (1.10) |
となる。
|
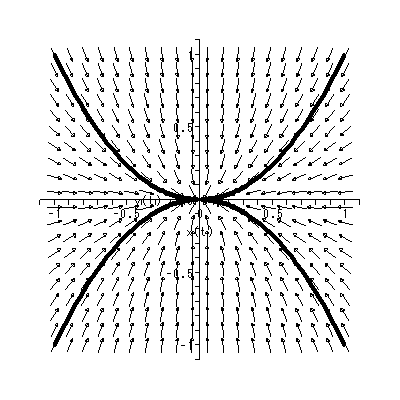
|
一方、行列 F1 、 F2 、 ・・・ は、
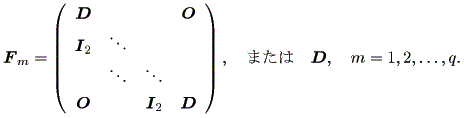
| (1.11) |
ここで、
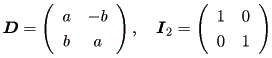
| (1.12) |
もちろん、 D の固有値は、 λ = a± bi 。
|
|
これらの結果から、もし A の次数が2ならば、 A の実標準形は、つぎの 3種のいずれかとなる:
(a)
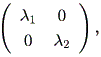
|
(b)
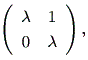
|
または、
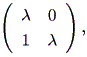
|
(c)
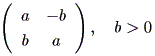
|
または、
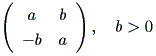
|
したがって、この場合、 (1.8) 式の解
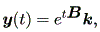
| (1.13) |
は、これらの3種のパターンに従い、つぎのようになる:
Case (a) 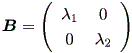
この時、 (1.8) 式は、
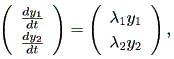
| (1.14) |
と単純化され、各次元ごと1次元線形微分方程式の解、 (1.2) 式の形となるので、
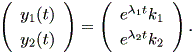
| (1.15) |
(1.15) 式から、次式も成り立つ:
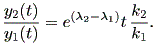
| (1.16) |
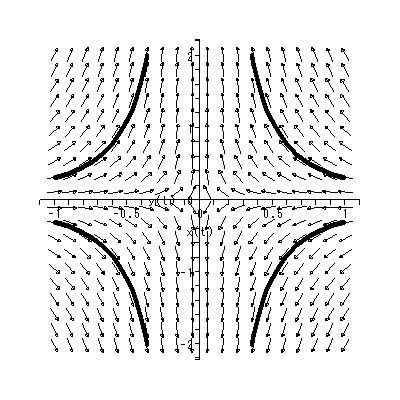
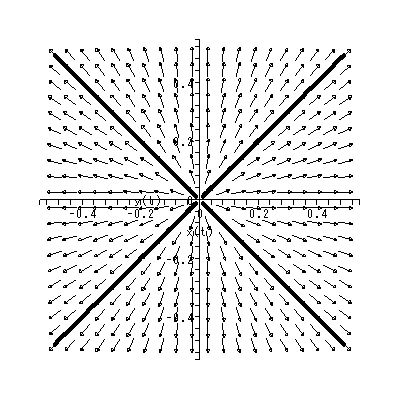
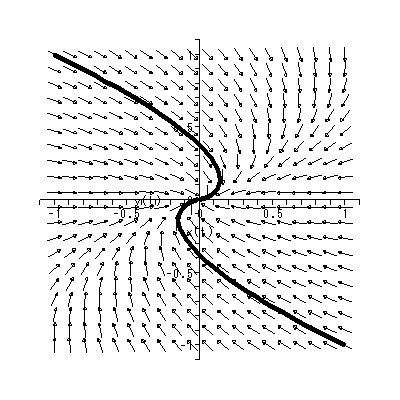
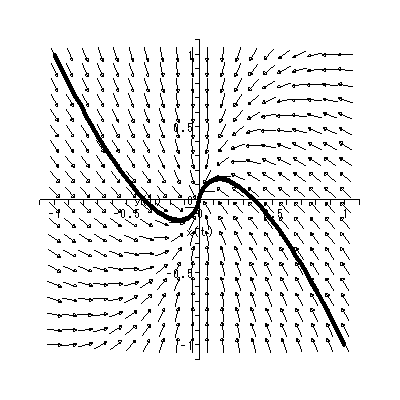
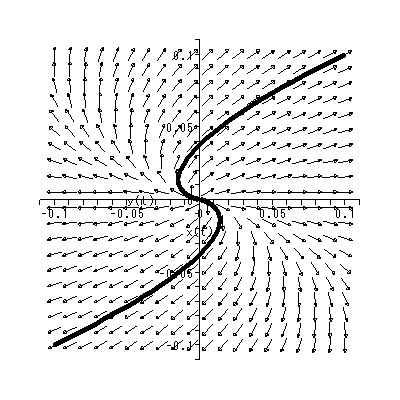
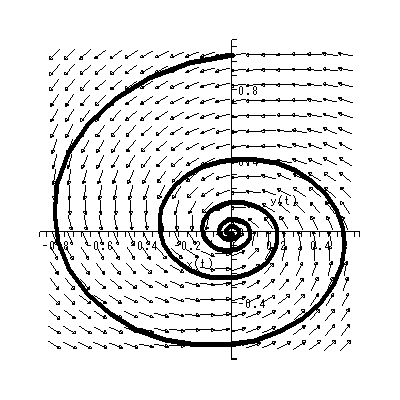
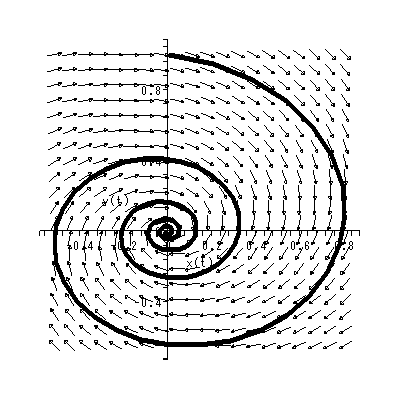
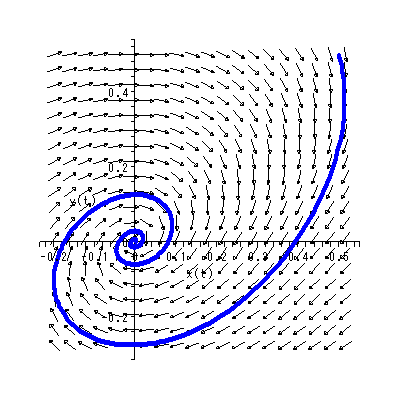
(1.15)、 (1.16) 式より、まず λ1≠λ2 の場合、固定点の近傍での解 曲線の特徴は、 λ1 、 λ2 の値に応じて、鞍点 (saddle) (図 1.2、1.3)、(内向)結節点 (inward node)(図 1.4、1.5)、または (外向き)結節点 (outward node)(図 1.6、1.7)となる。
一方、 λ1 = λ2 の時には、 (1.16) 式は、つぎのような特別な形
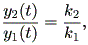
| (1.17) |
を取る。この式の特徴は、解曲線の時間 t での横軸座標値 y1 (t) に対する縦軸座 標値 y2 (t) の比が、初期点 k1 、 k2 に依存するものの、一定である、という ことであり、図 1.8、1.9 のような固定点の近傍での解曲線の特徴を示すことがわか る。これらは、焦点 (focus) と呼ばれる。
Case (b) 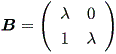
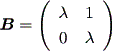
まず,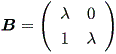
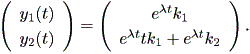
| (1.18) |
(1.18) 式は、以下のようにして導くことができる:
|
|
まず、Case (b) の最初のケースにおける行列 B から、
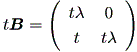
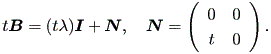
|
このとき、
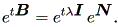
|
|
|
ここで、一般に
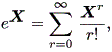
|
に注意すると、 etλI = etλI 。また、 N2 = N3 = ... = O なので、 eN = I+N 。そこで、
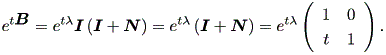
|
したがって、
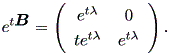
|
つぎに、 (1.18) 式より、
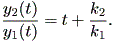
| (1.19) |
|
|
一方、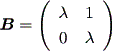
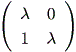
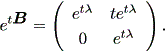
| (1.20) |
そこで、解曲線は
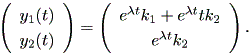
| (1.21) |
|
|
これより、
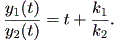
| (1.22) |
(1.19) 式および (1.22) 式から、 t → ∞ で軌道が固定点(原点)に近づく と、以下が成り立つ:
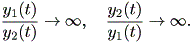
| (1.23) |
これらは、図 1.10 および図 1.11 にそれぞれ対応する。一方、 λ > 0 の場合、 図 1.12 もしくは図 1.13 は明らかである。これら4つの固定点は、仮性(或い は変格)結節点 (improper node) と呼ばれる。
Case (c) 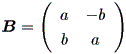
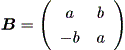
まず、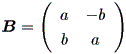
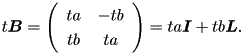
| (1.24) |
ここで、
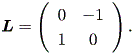
| (1.25) |
(1.24) 式より、
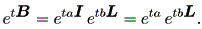
| (1.26) |
ここで、 etbL は、 L が2次の行列では、つぎのように書ける:
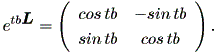
| (1.27) |
(証明)
まず、
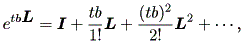
|
および、
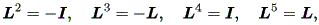
| (1.28) |
に注意(5回のベキ乗で、 L はもとに戻る!)し、 cos (tb) 、 sin (tb) の テーラー展開に注意すればよい。(証明終わり)
(1.26) 式および (1.27) 式から
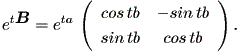
| (1.29) |
これより、解軌道の方程式は、
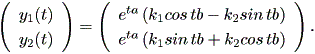
| (1.30) |
また、これより、次式も成り立つ:
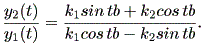
| (1.31) |
(1.30) 式から、 | cos tb | ≦ 1 かつ | sin tb | ≦ 1 に 注意すれば、 a<0 の時は limt→ ∞ y (t) = 0 。
一方、この曲線が y1 軸を横切る時の接線は、
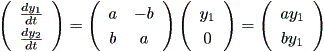
| (1.32) |
したがって、この時の y2 方向の微係数は、
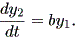
| (1.33) |
これらより、 b > 0 とすれば、 y1 > 0 → dy2 / dt > 0 、一方、 y1 < 0 → dy2 / dt < 0 となり、左巻きの spiral であることがわかる(図 1.14)。一方、 b < 0 なら ば、明らかに右巻きの spiral である(図 1.15)。ただし、この時、 y2 = 0 の時 の軌道は、 dy2 / dt = - b y1 なので、注意が必要である。 これらは、渦状(沈)点 (spiral sink) と呼ばれる。
これに対して、 a > 0 の時は、 limt→ ∞ y (t) = ∞ も明らか である(図 1.16 や図 1.17)。これらは、源点 (source) と呼ばれる。
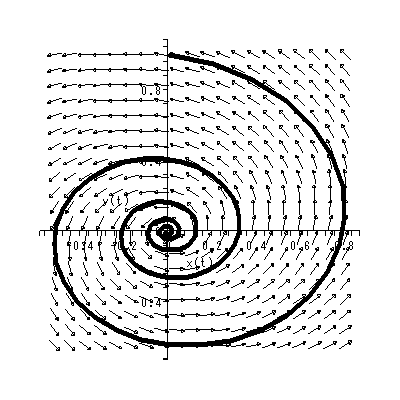
|
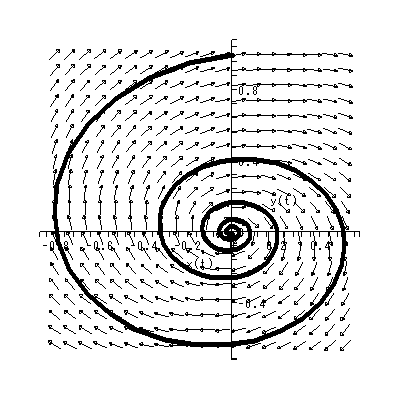
|
Case (c')
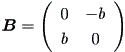
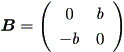
これは、Case (c) で a = 0 の特別なケースとみれるので、 (1.30) 式より、解 曲線は、
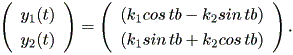
| (1.34) |
また、 (1.34) 式から、 y12 (t) + y22 (t) を求めると、
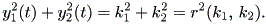
| (1.35) |
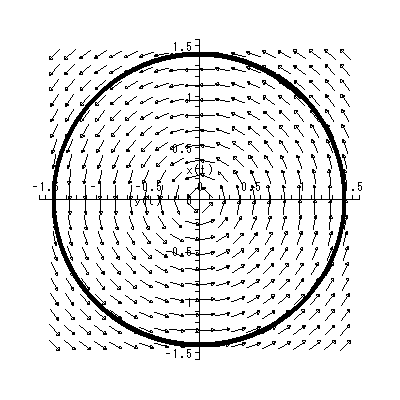
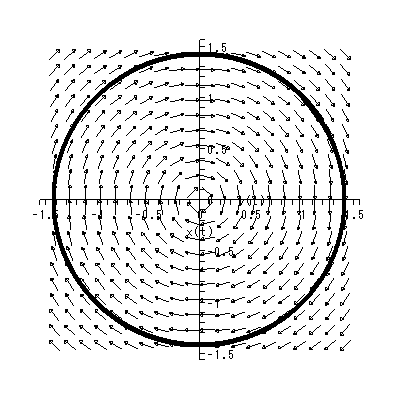
となり、初期点 (k1, k2) に依存した円の方程式であることがわかる。
一方、円軌道の回転の方向は、Case (b) の場合と同一なので、明らかである(図 1.18、図 1.19)。これらは、渦心点 (center) と呼ばれる。
|
|
最後に、上記の幾つかの特異点の呼称についてふれる。一般に、行列 A の固有 値が 負の実部 (negative real parts) を持つ場合、沈点 (sink) と呼 ばれる。したがって、内向き結節点、内向き仮性結節点、内向き焦点、および渦状 沈点は、すべて沈点に属する。
これに対して、行列 A の固有値が 正の実部 (positive real parts) を 持つ場合、源点 (source) と呼ばれる。したがって、外向き結節点、外向き仮性 結節点、外向き焦点、および渦状源点は、すべて源点に属する。
これまでは、 (1.5) 式の線形一次微分方程式系の特別なケース、すなわち n = 2 のケース(すなわち、平面上の力学系あるいは流れ (flow))を扱ってきた が、ここでは (1.5) 式の一般の線形系に話を戻し、そこでの流れの特性にふれる。
一般に、 (1.5) 式で表される線形系の原点 x = 0 は、前節の2次元系の場合 と同様、もし行列 A のすべての固有値が負の実部を持つならば、沈点と呼ばれ、 線形な流れ etA は縮小型 (contraction) と呼ばれる。
一方、もし行列 A のすべての固有値が正の実部を持つならば、原点と呼ばれ、 線形な流れは拡大型 と呼ばれる。
線形系における解軌道の長期的な振る舞い (the long-run behavior) は、 両者で大きく異なる。縮小型の流れは、漸近的安定 (asymptotically stable) 、拡大型の流れは、不安定 (unstable) であることがわかっている。あとで 詳しく述べるが、大雑把には平衡点はもしその近くの解が将来にわたっても近くに とどまる時安定、そうでない時不安定と言われる。
拡大型と縮小型を含めた流れは、双曲型 (hyperbolic flow) と呼ばれる。 この時、行列 A の固有値は非ゼロ実部 (nonzero real part) を持つ。 双曲型の流れに関しては、つぎの定理が知られている(例えば、Hirsch & Smale, 1974, p.151):
定理1 etA は双曲型流れとする。 この時、状態空間 E は、 A のもとで不変な直和分解 (direct sum decomposition)
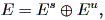
|
に一意的に分解できる。ここで、 Es 上の流れは縮小型、 Eu 上の流れは拡大型 である。
これまでに見てきたすべての特異点は、対人的相互作用の場を考える時、1つの心理 学的解釈が可能である(千野、1991, Chino, 1987; Chino & Nakagawa, 1990)。ま ず図 1.2 および図 1.3 の鞍点は、心理学的場を前者では上下に、後者では左右に分け る 心理学的障壁 の役割を果たす、と解釈できる。
図 1.4 および図 1.5 の内向き結節点の場合、一種の小集団の形成過程と見ること ができよう。ただし、あとで述べる渦状(沈)点と異なり、小集団の中心への接近 の仕方が相対的にストレートである。接近が最もストレートなのが図 1.8 の内向き 焦点である。これと、対照的なのが図 1.6 および図 1.7 の外向き結節点、および 図 1.9 の外向き焦点である。
内向き・外向き結節点や同焦点と似通ってはいるが、多少接近や回避の仕方の 異なるのが、図 1.10 および図 1.11 の 内向き仮性結節点である。この場合、 特異点への接近に、多少の回転が加わっている。いわば魅力の中心に接近する場合、 少し躊躇しながら接近するような場、と見ることができよう。これらと 対照的なのが、図 1.12 および図 1.13 の外向き仮性結節点である。
これらに対して、大きく回転が加わっているのが、図 1.14 および図 1.15 の 渦状沈点であり、魅力の中心に向かって回転しながら(躊躇しながら)徐々に 接近していくような心理学的場の特徴を持つ。これらと対照的なのが、図 1.16 および図 1.17 の渦状源点であり、回避の中心から躊躇しながらも徐々に 離れていく心理学的場の特徴を持つ。言い換えれば、下位集団の分解過程 と解釈できよう。
最後の、図 1.18 および図 1.19 の渦心点は、興味深い。すなわち、対人的 な接近・回避行動としては、center のような心理学的場は、魅力あるいは憎悪の 中心から接近することも回避することもなく、ぐるぐるとまわるようなアンビバ レントな心理学的場 を表している、と解釈できよう。
1.1.2 節では、 (1.5) 式で示される線形一次微分方程式系を扱った。その場合、特異点 の近くでの系の振る舞いは、係数行列 A の固有値により決定できることがわか った。それでは、一般の 非線形一次微分方程式系 (a system of nonlinear first-order differential equations) の場合、特異点の近くでの系の振る舞いは、 どのようにして検討できるのであろうか。
そのためには、つぎのようにして、系を特異点の近傍で線形化 (linearize) してやればよい(例えば、Guckenheimer & Holmes, 1983, pp.12-13)。 そのまえに、まず非線形一次微分方程式系をつぎのように定義することにしよう:
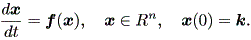
| (1.36) |
まず、 (1.36) 式の平衡点(したがって、固定点、特異点、浮動点でもある) x* は、 f (x*) = 0 なる点である。
(1.36) 式の特異点の近くでの解曲線の振る舞いは、 f (x) の特異点 x* における ヤコビアン あるいは、ヤコビ行列 (the Jacobian matrix) Jx* により線形化された系
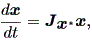
| (1.37) |
を調べてやればよい。ここで、
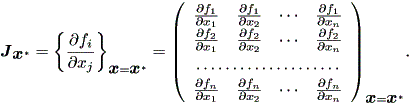
| (1.38) |
一般に、 (1.36) 式で表される非線形系の平衡点 x* は、線形化された系 (1.37) 式におけるヤコビアンのすべての固有値が負の実部を持つならば、沈点 と呼ばれる。非線形沈点は、局所的には線形沈点のように振舞う。
ただし、上記非線形系の特異点の近傍での系の振る舞いは、ヤコビアンがどの ような場合でも決定できるわけではない。後続の節「構造安定性」で述べるように、 これが可能なのは、特異点でのヤコビアンの固有値が 非ゼロ実部 (non-zero real part) を持つ場合に限ることが知られている。さもなければ、われわれは 系の線形化によっては系の振る舞いを決定できない。いわゆる構造安定性の議論 が存在するからである。実際、例えば渦心点だけは、固有値の実部がゼロなので、 正確には原理的に観測できない。実際、図 1.18 も図 1.19 も、コンピュータにこ れを描かせても、丸めの誤差を伴うので、正確には円にはならない。
構造安定性とは異なる概念に、系の平衡点の(リアプノフ)安定性 ( (Liapunov) stability of an equilibrium point) の概念がある(例えば、Hirsch & Smale, 1974, Chapter 9)。既に、前節の後半で、線形系に関する解軌道の長期的 振る舞いとして平衡点での安定性の問題に少しだけふれたが、ここではそれを含めた 一般の非線形一次微分方程式系に関する解軌道の長期的振る舞いについてふれる。
定義1 x* ⊆ W は (1.36) 式で表される非線形一次微分方程式系の 平衡点であり、 f: W → E はベクトル空間 E の開集合 W から E への C1 写像 (continuously differentiable) であるとする。もし、 W における x* のどんな近傍 U に対しても、すべての t > 0 に対して、初期値 x (0) のどん な解 x (t) も定義され、かつ U に含まれるような、 U 内の x* の 近傍 U1 が存在するならば、平衡点 x* は 安定 (stable) である。
定義2 平衡点 x* が、定義1での性質に加え、 さらに U1 が limt→ ∞ x (t) = x* と選べるならば、 漸近的安定 (asymptotically stable) である。
定義3 平衡点 x* が安定でなければ、 不安定 (unstable)である。この場合、 U 内の x* のどんな近傍に対しても、 x (0) ⊆ U1 から出発し、 U 内のどこにもないような少なく とも1つの解 x (t) が存在する。
これらの定義から、
|
ことが証明できる。線形系の場合と同様、平衡点 x* はヤコビアンの固有値が 非ゼロ実部を持つ場合(すなわち、沈点か源点の場合)双曲的と呼ばれるが、双曲的 平衡点はそれ故に不安定か漸近的安定かのいずれかであるといえる。
平衡点(特異点でもある)の解釈は、古くから例えば生物学における形態形成 (morphogenesis) の分野でなされてきた(例えば、Rosen, 1970)。とりわけ、形態形成 の基本的問題である最初均質な細胞の塊がどのようにして分化した特性を獲得していく かに関して40年代から50年代にかけて提案されたラシェフスキー・チューリング の理論 (the Rashevsky-Turing theory) (Rashevsky, 1940, Turing, 1952, Waddington, 1957) によれば、細胞の初期の均質な状態は不安定な平衡 (unstable equilibrium) 状態であり、やがてそれは不規則な動揺により平衡状態か ら外れ、明確に定まった 漸近的安定 (asymptotically stable) 状態に向か うという。
生物学では、系の最終状態が、初期状態の如何に無関係な場合、系は等終局性 (equifinality) を持つと呼ぶ (Rosen, 1970)。その意味では、まさに漸近安定性 (asymptotical stability) は、生物学における等終局性に対応している。
ただし、ここで注意が必要である。(リアプノフ)安定性は、あくまでも特定の系 における状態変数の値を漸近的安定な平衡点(あるいは特異点)の近くで攪乱させた 場合、つまり、初期値を変えた場合長期的には状態変数の値は特異点に収束していく かどうかという議論である。したがって、漸近安定性の議論では、系自身(より正確 には系の方程式自身)は変わらないことを前提にした議論である点に注意が必要であ る。
これに対して、後に述べる構造安定性の議論は、系自身を攪乱した場合、系の特性( すなわち系の方程式自身)が変わるか変わらないか、の問題であり、(リアプノフ) 安定性とは異なる概念である。もちろん、構造安定性の問題も、後に見るように、生物 学の形態形成の分野では本質的なものと考えられている。
漸近的安定な平衡点以外に、生物学的解釈がなされる重要なものに鞍点がある。前節 では、線形系の場合の鞍点が心理学的には一種の心理学的障壁と解釈できるというこ とを述べたが、鞍点は生物学的にも同様の概念、すなわち 閾値現象 (threshold phenomenon) として解釈されている (Rosen, 1970, p.196)。
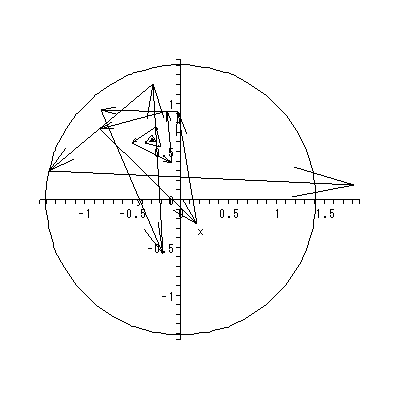
ただし、ローゼンでは、単なる線形系の鞍点ではなく、多くの定常状態を持つ 開放系 (multiple steady states in open systems) という文脈で、鞍点以外に多 くの平衡点(特異点)を持ちかつ鞍点の左右に漸近的安定な平衡点がある場合の鞍点 に関して、議論がなされている。そのような場は、図 1.20 のよう な場で、第2象限の鞍点に対応する。
すなわち、図 1.20 の場合、第2象限の鞍点の近くで、もし初期状態が鞍点の少し 右上の場合は、長期的には状態は第1象限の渦状沈点に収束していくのに対して、初期 状態がもし鞍点の少し左下にある場合は、状態は長期的には第3象限の渦状沈点に収束 していく。つまり、初期状態をわずかに変化させることにより、最終状態に大きな変化 がもたらされるわけである。
|
ローゼン (Rosen, 1970, pp.196-197) は、生物の形態形成過程で卵の一見均質な塊 の中から、皮膚、神経、筋肉などが次第に分化していく過程についてのワディントン (Waddington, 1957) の隠喩すなわち 後成的風景 (epigenetic landscape) に ついての説明を、ワディントンの著書を引用する中で、行なっている。
実は、この図は、後に述べるように、対人相互作用による対人関係の遠近関係 の推移を縦断的ソシオマトリックスから推定する DYNASCAL (Chino & Nakagawa, 1983, 1990) による特定の時点での推定ベクトル場のイラストのために描いたもの である。千野が DYNASCAL を提案する端緒となったのは、ローゼンによる上記ワデ ィントンの後成的風景についての多重定常状態の図からヒントを得たことにある。 また、DYNASCAL における場の考え方は、いうまでもなくレビン (例えば、Lewin, 1933) の場理論からヒントを得たものである。
これまで、線形系や非線形系での特異点(平衡点)の一般的な分類について議論して きたが、ここでは孤立系や閉鎖系での特異点(平衡点)の特徴について紹介する。 まず、孤立系 (isolated system) とは、一般に外界に対して、エネルギーも 物質も交換しない物質系をいう。これに対して、閉鎖系 (closed system) とは、 外界に対して、エネルギーは交換するが、物質の交換をしない系をいう。閉鎖系は、 孤立系の意味に用いられることもある。
ローゼン (Rosen, 1970, pp.111-116) は、状態変数が2次元(2変数の)化学物質 の濃度である場合の一次線形系で、外界から如何なる化学物質も系に入らない閉鎖系
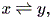
| (1.39) |
の場合を考察し、その意味での保存場ないしは閉鎖系では (1.5) 式の行列 A の 固有値の1つはゼロとなること、また他方の固有値は閉鎖化学系としての特異点の漸近 安定な性質から負となることが要請されることなどを述べている。
この場合の系の特徴は、前節の2次元線形系の3種類のケースでは Case (a) の特殊 な場合であり、沈点でも源点でもないし、また渦心点でもない、いわゆる退化特異点の 1種である。このような系の軌道特性を示したのが、図 1.21 である。この図では、 特異点は、原点を通る直線 y = (5/3) x 上に無限個並んでおり、系はつぎの式で表され る:
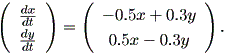
| (1.40) |
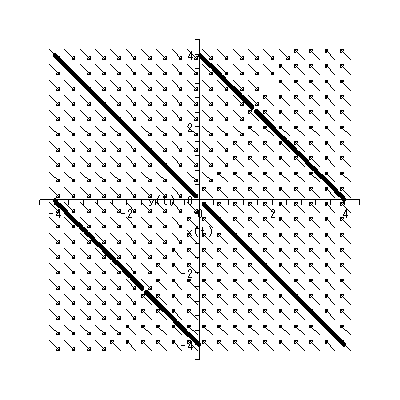
|
この系は、ローゼンが述べているように、興味深い挙動を示す。すなわち、任意の 特異点(平衡点)上に状態変数が位置する、すなわち平衡状態にあるこの閉鎖系の状態 変数の1つを攪乱させると、系はその攪乱に反抗するように新たな平衡(平衡点)へと 動いていく。
注意すべきは、このような系では Case (b) のような仮性結節点ばかりではなく、複 素固有値は現れないため、Case (c) のような図 1.14 や 1.15 の渦状沈点や図 1.16 や 1.17 の渦状源点も、さらには Case (c') の過心点も、決して現れることはない点 である。さらに、このような系は、後に見るいわゆる構造不安定な特異点に属すると いう点である。したがって、このような系は系自身の攪乱により、全く軌道特性の異 なる系になるので、誤差を含む如何なる観測によっても観測は不可能である点である。
一方、うえのような化学的平衡状態にある系ではなく、力学的平衡状態にある系の 1つである保存場(運動エネルギーと位置エネルギーの和が一定であるような場)は、 いわゆる 勾配ベクトル場 (gradient vector field) の特徴を持ち、その性質 から特異点でのヤコビアンは実対称行列になるので、必ず実数固有値により対角化 できる。すなわち、固有値としてジョルダンブロックや複素根は現れない。このこと は、保存場ではやはり化学的平衡な上記の線形系と同様、仮性結節点、渦状沈点、渦 状源点、渦心点も存在しないことを意味する。エネルギー保存則の成り立つ系は、 より一般的には ハミルトン系 (the Hamiltonian system) と呼ばれるが、 エネルギーの損失が起こる系、すなわち 散逸系 (dissipative sysem) の方が 多様な系の振る舞いを示すことを示唆する性質である。
前節では、非線形一次微分方程式系における局所的な系の振る舞いとして、系を 特異点で線形化し、非退化特異点の近傍での系の振る舞いを見てきたが、一般の 非線形系では、特異点以外によく知られたものに、リミットサイクル (limit cycles) がある。リミットサイクルは、渦状沈点または渦状源点の周り に閉軌道 (closed orbit) を伴う。リミットサイクルには 2種類あり、1つはアルファリミットサイクル ( α- limit cycle) 、 もう1つはオメガリミットサイクル ( ω- limit cycle) と呼ばれる。
アルファリミットサイクルは、閉軌道外側の近傍ではそこから徐々に離れていく 軌道、および閉軌道の内側の近傍でもそこから徐々に離れて内側に存在する渦状沈 点にひきつけられていく軌道を伴う。両方の軌道とも、時間をどんどんさかのぼ ると無限に閉軌道に近づく。
オメガリミットサイクルは、閉軌道の外側では遠くから閉軌道に外側から無限に 近づく軌道と、閉軌道の内側の渦状源点の近傍から出発して閉軌道に内側か ら無限に近づく軌道から成る。
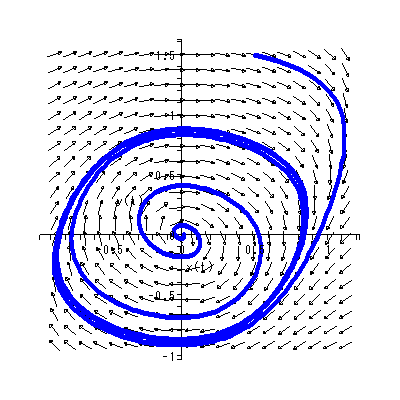
|
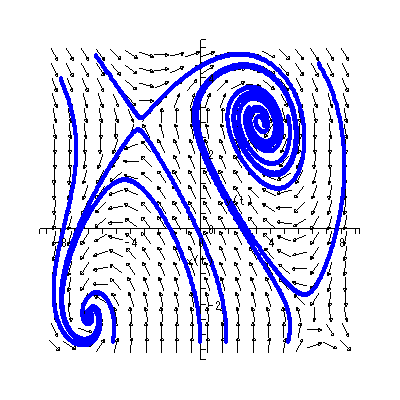
図 1.22 のリミットサイクルは、Hirsch & Smale (1974, pp.227-228) で紹介 されている電気回路の物理的特性を記述する非線形自励微分方程式系で、分岐パラメ ータの値 μ = 0.5 のケースを Maple で描いたものである:
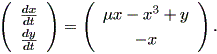
| (1.41) |
図では、原点が渦状源点であり、原点の近傍から出る解軌道は卵型の閉軌道に無限に 近づいていく。一方、卵型の閉軌道の外から出発する軌道は、図のように閉軌道の外側 から閉軌道に対して無限に近づいていく。閉軌道上での動きはこの場合、右廻り(時計 廻り)である。この系の軌道特性は、この分岐パラメータ μ の値が連続的に変化 するとき、劇的に変わる。この種の問題は、次節で述べるベクトル場の特異点の分岐理 論で議論する。
物理学、化学、や生物学の分野では、リミットサイクルはよく知られている。例えば (1.41) 式で表される系は、電気回路の状態を表す2次元の非線形系の例であり、 x は回路を流れる電流で、 y は電圧である。また、 μ は回路の抵抗の特性(例え ば抵抗の温度)にかかわるパラメータである。この系のヤコビアンの計算から、 -1 ≦ μ ≦ 1 の仮定のもとでは、 -1 ≦ μ < 0 の時特異点は渦状沈点 となり、長期的には電流、電圧ともどんどんゼロに近づいていくので、回路は死に 至る。一方、 μ = 0 になると、ヤコビアンの値はゼロ(さらに両固有値ともゼロ) で退化特異点となる。また、この値を超えて 0 < μ ≦ 1 になると、特異点は 渦状源点となり図にあるようなリミットサイクルが現れる。この場合、回路は "蘇生 して" (電流も電圧も)振動し始める。いわゆる 発振器 (oscillator) と なる。
生体分子とりわけ RNA や DNA のような 情報分子 (information molecules) が複数あり、それらが 触媒連鎖 (catalytic chains) をなす場合の Eigen and Schuster (1977a, 1977b, 1977c) による ハイパーサイクル (hypercycles) のモデルでは、 n 個の分子の濃度の変化についての微分方程式モデ ルが、 n ≧ 5 の場合、安定したリミットサイクルを持つことが示されている。こ のことは、そのような系では、すべての分子が長期的に増えたり減ったりし振動する ことを意味し、分子の組の現存するすべての情報が、長期にわたり維持されることに なる (Rowe, 1994, p.95)。
中野 (1990) に紹介されている、Amari (1972) による相互結合のある2細胞の神経 回路の膜電位 x 及び y に関するつぎの非線形微分方程式系でも、ある条件下で はリミットサイクルが存在することが報告されている:
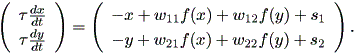
| (1.42) |
ここで、 τ は時定数、 wij は細胞 Cj から細胞 Ci への結合加重を 表し、抑制性の結合の場合負の値をとるものとする。また、 s1 及び s2 は細胞 C1 及び C2 への外部出力、 f (x) は x → ± ∞ でそれぞれ 1 及び 0 をとるシグモイド形の出力関数である。
Amari (1977) は、マカロック・ピッツのニューロン (McCulloch-Pitts formal neuron) の原理に従った連想と概念形成のモデルを提案する中で、例えば 概念形成 (concept-formation) は、複数のニューロンが自己組織化する中で複数 の特異点を形成する系を創出することであり、このようなメカニズムは 短期記 憶 (short-term memory) に属するとする。一方、長期記憶 (long-term memory) は、これらに関与したシナプス重み (synaptic weights) の変化に 対応するとする。
また、Tsuda (1991) はニューラルネットワーク、とりわけ神経回路の非線形 振動子 (nonlinear oscillator) に関する考察から、われわれの知覚 (perception) は力学系の固定点であり、概念 (concept) はリミットサイクル、トーラス、カオス などの振動活動であろう、と述べている。
社会行動科学の分野、とりわけ心理学の分野では80年代から力学系の理論の応用が次 第に注目を集めつつある(例えば、Heath, 2000)が、まだ十分知られているとは言 いがたい。
千野ら (Chino, 1987; 千野, 1991; Chino & Nakagawa, 1991)は、リミットサイ クルおよびその分岐(正確には、後に述べるホップ分岐)を、小集団の形成過程の 文脈で、社会心理学的に解釈可能であることを指摘している。実際、アルファリミ ットサイクルや、図 1.22 の オメガリミットサイクルにおける特異点の周りの閉軌 道は、小集団におけるある時点での下位グループとそれ以外を分ける境界と 見なすことができよう。とりわけ、アルファリミットサイクルでは、閉軌道の内側 では中心の特異点(渦状沈点) に向かう軌道特徴が見られ、閉軌道の外側では閉軌 道から遠ざかる渦状源点の軌道特徴が見られるので、下位グループ以外の成員を寄 せ付けない閉鎖的な下位集団の形成過程と見なすことができよう。
1.1.1 節の註3で紹介した高階微分方程式にも各種の形が存在するが、ここでは まず、 n 次微分までを含む線形微分方程式
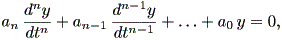
| (1.43) |
について述べる。
この形の n 階微分方程式は、次の変換により線形一次微分方程式系として書き 直すことができる:
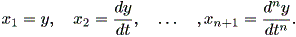
| (1.44) |
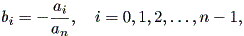
| (1.45) |
とする。
この時、まず (1.45) 式を用いて、 (1.43) 式を変形すると、
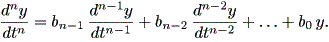
| (1.46) |
つぎに、 (1.44) 式なる変換により、

| (1.47) |
とするものとする。この時、 (1.46) 式は、 (1.5) 式と同様、
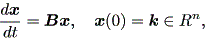
| (1.48) |
と書ける。ここで、行列 B は、
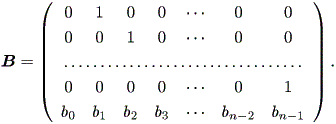
| (1.49) |
行列 B は (1.46) 式を
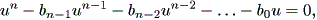
| (1.50) |
なる n 次方程式と見なした場合の同伴行列 (a companion matrix) で ある。
いずれにせよ、高階微分方程式のうち、 (1.43) 式の形をしたものは、 (1.48) 式の線形一次微分方程式系に等しいので、1.1.2 節での述べた方法で、系の振る舞い を簡単に調べることができることに注意したい。
これまで述べてきた高階線形微分方程式に対して、非線形高階微分方程式の中には、 歴史的に見て古くから数理物理学や工学などの自然科学の分野で頻繁に研究され応用 されてきたものがある。それらは、いわゆる ダッフィング方程式 (Duffing's equation) とファンデルポール方程式 (van der Pol's equation) である。 これらは、最近では心理学の分野でも取り上げられつつあるので、ここでも簡単に 紹介する。
その前に、これらの方程式のもとになっている調和振動子 (the harmonic oscillator)、及び両方程式をその中に含むところのリエナール方程式 (Li'enard's equation) にふれる。
直線上の原点から x の位置に質量 m の質点があるとする。この質点が原点に向 かう力 F (x) を受けており、 F (x) = - m p2 x であると仮定する。ここで、 p は 定数である。ここで、ニュートンの第2法則 (Newton's second law) 、すな わち、 F (x) = ma = m (d2x / dt2) に注意すると、
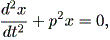
| (1.51) |
が成り立つ。この運動モデルが調和振動子と呼ばれるものである。
調和振動子の具体例は、平面内の単振子 (the simple pendulum) で sin x を x で近似したとき、あるいはばねの力等による質点の運動などにより得られる。
これまでの議論は、例えば単振子であるならば、空気の摩擦力などの力が入らない 場合である。一方、摩擦を考慮すると、単振子の運動モデルは、つぎのようになる:
すなわち、まず質量 m なる質点が長さ l の針金の先端についているとして、 針金の垂直方向からの角度が θ であるとする。この時、振り子の角速度は dθ / dt 、速度は l dθ / dt である。この時、質点に働く接線方向の摩擦 力は - kl dθ/dt (k ≧ 0) である。
一方、質点に働く主要な力は重力であり、振り子がふれるときその接線方向の成分 は、 - m sin θ である。そこで、接線方向の力の合計は、
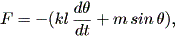
| (1.52) |
と書ける。また、接線方向の振り子の加速度は l d2θ / dt2 である。 これらより、
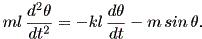
| (1.53) |
これより、
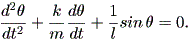
| (1.54) |
ここで、左辺第2項は、振り子の空気抵抗により生ずる摩擦力に依存する部分であり、 同左辺第3項は、振り子にかかる重力の接線方向の成分に依存する部分であることに 注意されたい。
(1.54) 式の θ を x で置き換えると、
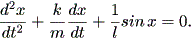
| (1.55) |
ここで、摩擦がゼロ、すなわち k = 0 でありかつ sin x = x とすると、 (1.51) 式で表される調和振動子となる。
つぎに、バネによる質点の運動モデルについて見てみよう。質量 m の質点には 小さな車輪がついており、近くの壁からバネとダッシュポット (dashpot) で つながれているとする。ダッシュポットとは、ピストンをはめたシリンダーに流体 を出し入れさせ、速度に比例した抵抗を与える装置である。この時、壁から質点まで の距離を x とする。
この時の質点の運動方程式は、
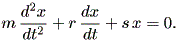
| (1.56) |
ここで、 r は、減衰係数 (damping factor) 、 s はスプリングの スティフネス (stiffness) に関する定数である。この系は、抵抗の存在により、 あとで見るように、減衰線形振動子 (damped linear oscillator) となり、 散逸力学系の最も単純な例である。
摩擦のある振り子の運動方程式 (1.55) 式と、抵抗のあるバネにつながれた質点 の運動方程式 (1.56) は、同じ形になることがわかる。
前節で見た調和振動子や線形減衰振動子は、どのような系の振る舞いを示すので あろうか。まず、調和振動子の場合、 (1.51) 式は
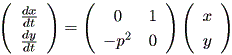
| (1.57) |
と2次線形系の形に書きなおせる。この2次線形系は、係数行列の固有値が λ = ± p i となるので、2次元的には渦心点となる。ただし、 (1.57) 式の係数行列は、 前節の議論から、このような2次線形系に直さずとも直接 (1.51) 式から (1.49) 式の 同伴行列を計算しても同じ結果になることに注意せよ。
したがって、 (1.34) 式より、
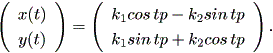
| (1.58) |
そこで、 x については、
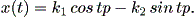
| (1.59) |
そこで、初期点 (k1, k2) を
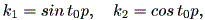
| (1.60) |
として選べば、
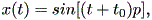
| (1.61) |
と書ける。
いずれにせよ、 x (t) は正弦波とみれる。すなわち、摩擦もしくは抵抗のない場合、 あるいは調和振動子では、減衰のない (undamped) 振動子となる。
(註1) Hirsch and Smale (1974, p.16) では、 (1.58) 式の形、Thompson and Stewart (1986, p.38) では、 (1.61) 式の形の解が示されているが、本質的には 同一である。
一方、摩擦ないしは抵抗がある場合は、 (1.56) 式を簡略化して、
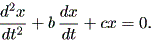
| (1.62) |
この式を dx / dt = y と置いて変換すると、
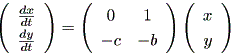
| (1.63) |
と書ける。この線形系の係数行列の固有値は、
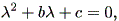
| (1.64) |
の根であり、
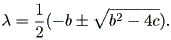
| (1.65) |
(1.56) 式と (1.62) 式との関係から、 (1.65) 式の係数 b はダッシュポットの 減衰係数、 c は弾性スプリングのスティフネスにかかわることに注意しよう。
b と c をいろいろ変えると、それに応じて 1.1.2 節で述べた特異点のいず れにもなり得る。例えば、図 1.14 や図 1.15 のような特異点、すなわち渦状沈点 となれば、減衰振動する。これらの詳細については、例えば Thompson and Stewart (1986) を見よ。
リエナール方程式は、Hoppensteadt (1993, p.32) によれば、
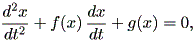
| (1.66) |
である。ここで、関数 f 及び g は x の連続関数である。
関数 f 及び g の満たすべきより正確な条件については Rosen (1970, pp.136-137) に記されている。
ローゼンでは、この方程式は2次元非線形系の形で2種類定義されており、 変数変換により他方を導くことができる。第1の定義は、
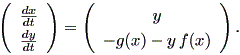
| (1.67) |
で、第2の定義は、 (1.67) 式を z = y + F (x) と変換することにより得られ、

| (1.68) |
ここで、

| (1.69) |
リエナール方程式は、リミットサイクルを1つだけ持つことがわかっている。証明に ついては、例えば Rosen (1970, pp.136-139) を見よ。
ダッフィング方程式は、Thompson and Stewart (1986) によれば、最初 Duffing (1918) により精力的に研究されたもので、現在では幾つかのバージョンが知られている。 例えば、伝統的なダッフィング方程式は、
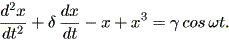
| (1.70) |
一方標準的ダッフィング方程式は、
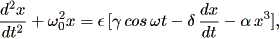
| (1.71) |
である。 (1.70) 式あるいは (1.71) 式は、減衰周期強制非線形振動子 (the damped, periodically forced nonlinear oscillator) と呼ばれることがある。
(1.71) 式で、強制振動項がない場合、ダッフィング方程式は、
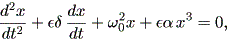
| (1.72) |
と書ける。
(1.72) 式は、明らかに (1.66) 式のリエナール方程式の特別のケースである。
ダッフィング方程式とよく似た形で、やはりリエナール方程式の特別な場合にあたると みなせるものに、ファンデルポール方程式がある。Thompson and Stewart (1986) によ れば、この方程式は最初 Rayleigh (1896) により導入され、その後 van del Pol (1927) により電気回路を用いて理論的にも実験的にも研究されたという。こちらも、 いろいろなバージョンが存在する。例えば、Thompson and Stewart (1986) では、フ ァンデルポール方程式は、
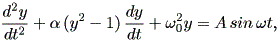
| (1.73) |
として定義されている。
一方、Guckenheimer and Holmes (1983) では、つぎのようにさらに一般的な形として 定義されている:
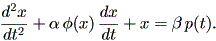
| (1.74) |
ここで、 φ (x) は偶関数で、 | x | < 1 の時負、 | x | > 1 の時 正、 p (t) は T - 周期的、 α 及び β は非負のパラメータである。 (1.74) 式は、自励系として、
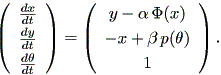
| (1.75) |
と書くこともできる。ここで、 (x,y,θ) ⊆ R2 × S1 である。
(1.73) 式で、 α ≧ 1 でかつ A = 0 の時、すなわち強制振動項がない 場合は、自励緩和振動 (self-excited relaxation oscillations) と呼ば れる。
Sprott (2003) の付録、とりわけ A.4 には、ダッフィング、ファンデルポール、 レイリーがらみやその他の各種振動子の例がリストアップされている。その中でも、 ダッフィング方程式の中に (dx / dt)3 の項のあるレイリー・ダッフィング 振動子 (Rayleigh-Duffing oscillator) を紹介する。この系は、
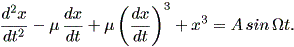
| (1.76) |
と書かれる。この系で、強制振動項がない場合は、
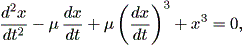
| (1.77) |
となり、それでも (1.72) 式と少し異なる。
心理学における力学系の応用に関しては、まえがきのところでも述べたように、 運動学習 (motor learning) の分野の研究が比較的多い。 その中で、例えば Nourrit et al. (2003) は、スキーシミュレータを使った縦断的研究で、練習の初期と後期で 被験者の行動に大きな違いがあることを見つけ、以下のような2つの力学系方程式を データに当てはめている。初期の段階では、前者のダッフィング方程式とレイリー (・ダッフィング)方程式を折衷したもの、後期の段階では後者のダッフィング方 程式とファンデルポール方程式を折衷したものが当てはまるという。
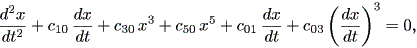
| (1.78) |

| (1.79) |
これまで見てきたように、非線形一次微分方程式系、とりわけ非線形2次元系では、 局所的な系の振る舞いとして、特異点およびリミットサイクルを紹介してきた。しか し、非線形系では、これら以外の系の振る舞いも数多く存在する。ハートマン・ グロブマンの定理 (Hartman & Grobman's theorem) によれば、非線形系のヤコビア ンが特異点で非ゼロ実部 (non-zero real part) を持つならば、すなわち、 ヤコビアンの固有値にゼロまたは純虚数となるようなものがないならば、場は 構造安定 (structurally stable) と呼ばれる。構造安定な系は、系を外から 多少摂動させても軌道特性は変わらないので、われわれはそのような系を観測する ことが可能である。
一方、構造不安定な (structurally unstable) な系は、系を外から少し摂動させ ても軌道特性が大きく変わるため、わずかでも誤差を伴うようであれば、原理的に観 測不能である。図 1.18 および図 1.19 では、一見解軌道は閉じた円のように見え るが、渦心点は、構造安定性の定義から明らかに構造不安定で、円のように 見えるのは、コンピュータに描かせた軌道が太いため、われわれの錯覚に過ぎない。
構造安定性の概念は、青木・白岩 (1985) によれば、最初 Antronov and Pontrjagin (1937) が小さな摂動に対しても軌道特性の変わらない系を「粗い系」と呼んだのに 対して、後に Lefschetz が命名したという。
前節および前々節では、線形系および非線形系におけるベクトル場の特異点とその 近傍での系の振る舞い(解曲線の特徴)を検討した。ここでは、そのような系の振る 舞いが、何らかのパラメータ(複数個)により変化するようなプロセスについて 見てみよう。数学では、このような問題はベクトル場の分岐 (bifurcation) の問題として知られている。一般に、非線形一次微分方程式系では、分岐パ ラメータ (bifurcation parameters) を c とベクトル表現すれば、系はつ ぎのように書かれる:
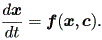
| (1.80) |
1.1.5 節であげた (1.41) 式は、この一般的な系の特殊例であり、分岐パラメータは その場合1つで、 c1 = μ である。
|
一般に、ベクトル場の分岐には2種類ある。1つは、特異点の近傍での系の振る舞い の変化に関するもので、局所的分岐 (local bifurcation) と呼ばれる。もう 1つは、特異点の近傍の系の振る舞いの変化ではなく、ベクトル場全体での系の振る 舞いの変化に関するもので、大局的分岐と呼ばれる(例えば、Guckenheimer & Holmes, 1983)。
非線形2次元自励系で分岐パラメータが1つしかない場合の局所的分岐としては、 従来サドル・ノード分岐 (saddle-node bifurcation) ピッチフォーク 分岐 (pitchfork bifurcation)、トランスクリティカル分岐 (transcritical bifurcation)、ホップ分岐 (Hopf bifurcation)、などがよく知られている。
例えば、サドル・ノード分岐は、分岐パラメータの連続的な変化により、あるパラ メータの値になると(特異点がない状態から)突然退化特異点がまず生まれ、その 後鞍点と結節点が生まれて成長するプロセスである。退化特異点は、もちろん 構造不安定であり、原理的に(少しでも誤差を伴う観測では)観測不能である。
ホップ分岐は、特異点の1つである 渦状沈点や渦状源点 の中心に、あるとき突 然退化特異点である小さな渦心点が生まれる。この渦心点の中心には、特異点が 渦状沈点の場合は渦状源点が、同じく渦状源点の場合は渦状沈点がそれぞれ生ま れ、分岐パラメータの値の連続的な変化にしたがって、閉軌道が次第に大きく成 長していくプロセスである。図 1.23 は、図 1.22 でのオメガリミットサイクル が成長してくる前(分岐前)の系の特徴すなわち、渦状沈点の状態を Maple に 描かせたものである。ちなみに、この場合の系、すなわち (1.41) 式の分岐パラ メータの値は、 μ = -0.5 であり、図 1.22 でのオメガリミットサイクルが現 れている系の分岐パラメータの値は、 μ = 0.5 である。分岐の瞬間は、理論上 は μ = 0.0 の場合である。
一方、大局的分岐には、サドルループ (saddle loop) や サドル結 合 (saddle connection) などが知られている。サドルループは、渦状沈点と鞍点 の対から成るベクトル場が、分岐パラメータの変化により、突然渦状沈点が渦心点 に変わり、さらに渦心点が源点に変化する場合をいう。サドルループでは、ベクト ル場の変化はある特異点(この例では、渦状沈点)の近傍のみにとどまらず、対と なっている鞍点とのかかわりでもベクトル場の特徴が変化する点が局所的分岐と異 なる点である。
サドル結合は、近接した2つの鞍点間のベクトル場の特徴が、分岐パラメータ の変化により、突然一方の鞍点から出る軌道が対の鞍点に入る軌道に変化し、そ の後2つの鞍点の位置を変えることにより、サドル結合が解ける場合をいう。
局所的分岐にせよ、大局的分岐にせよ、分岐の瞬間には退化特異点が生ずるが、 構造安定性の議論から、そのような分岐の瞬間は構造不安定で、原理的には誤差を 伴う観測によっては観測不可能である。
これまで紹介してきたいろいろなベクトル場の分岐についても、場合により、心 理学的解釈が可能である。例えば、千野ら(Chino, 1987; 千野, 1991; Chino & Nakagawa, 1990)は、ホップ分岐が社会心理学的に解釈できることを 示している。実際、例えば図 1.21 から図 1.20 への渦状沈点からオメガリミッ トサイクルへの分岐は、渦状沈点を下位集団の形成過程の1つと解釈すれば、 一旦形成されつつあった下位集団の芽が、何らかの分岐パラメータの連続 的変化により、その中心からしぼみだし、(オメガリミットサイクルの内側の渦 状源点により)崩壊しつつある過程、と解釈できる。
これに対して、アルファリミットサイクルによるホップ分岐は、渦状源点に より表されるベクトル場、すなわちそれまで他の成員が近づくことが出来なかった 心理学的場の中心に、何らかの分岐パラメータの値の連続的変化により、突然アルファ リミットサイクルが生じ大きくなっていくプロセスである。アルファリミットサイク ルの中心には渦状沈点があり、閉軌道の中は、小集団の形成過程と解釈で きるので、この場合のホップ分岐はそれまで他の成員が近づけなかった心理学的場の 中心に突然成員を惹きつける場が生じ、閉軌道すなわち閉鎖的な下位集団が成 長していく場と解釈することができる。
80年代以降、力学系の応用の流れは心理学の分野に限ってみても、欧米では徐々に 大きな潮流になりつつある。実際、例えば文献検索エンジンの1つである PsycINFO を使って "dynamical system" に関連する心理学の分野の文献を出力させると、平成 16年8月27日現在で、文献数は399にのぼる。
ここでは、それらのうち、地理学の分野および計量心理学の分野で開発された2、3 の研究を紹介する。それらは、力学系とりわけ微分力学系を帰納的、統計的方法によ り縦断的データからベクトル場として推定する方法であり、力学系の通常の適用の流 れとは異なるものである。
1つは、Tobler (1976-1977) による風モデル (the wind model) であり、 彼のモデルでは、地域間の人の移動などの非対称行列をユニークな方法で分析するも ので、各対象の位置は地理学的にあらかじめ定まっている。風モデルでは、対象間の 人の移動などの非対称行列に特定のモデルを仮定し、それを用いて対象間の風もしく は 流れ (flow) の方向と大きさを推定し、各対象ごとにそれらを合成し、 得られた2次元平面上で推定される推定ベクトル場を 非回転的場 (curl free part) と 非発散的場 (divergence free part) の2つに分解し、さらに前者 の別名 勾配ベクトル場 (gradient vector field) の スカラーポテン シャル (scalar potential) を数値計算法により推定し、コンピュータに描かせる ものである。
2つ目は、千野が80年代に共同研究者の中川や数学者の白岩の協力を得て、縦断的 非対称関係行列を手にした時、グループの成員間の対人的相互作用により生じると考 えられる心理学的力の場に2次元の一般非線形微分方程式系を仮定し、上記微分方 程式の定性理論や、構造安定性、さらにはベクトル場の 分岐理論 (bifurcation theory) を応用し、データから各時点でのベクトル場と特異点および そこから出入りする幾つかの解軌道を描き出す方法であり、DYNASCAL (Dynamical System Scaling) と呼ぶ(Chino & Nakagawa, 1983, 1990)。
DYNASCAL と一部類似の発想で、非対称行列からベクトル場を推定する方法を、 Yadohisa and Niki (1999) も提案しているが、DYNASCAL のように特異点やその軌 道特性までは出力しない。
トブラーは、千野 (1997) も解説しているように、対象の流れの方向と大きさを推定 するモデルとして、幾つかの例をあげているが、それらのうちの1つはつぎのようで ある:
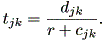
| (1.81) |
ここで、 tjk は地点 j から地点 k までに要する移動費用とか時間などの 移動コストである。また、 djk は2地点間の距離である。一方、 r は、位置 や流れの方向に依存しない移動速度である。最後の cjk は、移動速度である。
(1.81) 式で cjk = - ckj および tkj = dkj / (r + ckj) に注意すると、次式が導かれる:
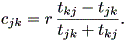
| (1.82) |
風モデルでは、この式での右辺の tjk を類似度行列の第 (j,k) 要素と見なし、 この式から各対象に働く流れの大きさと方向をまず推定する。詳細は、千野 (1997) を参照されたい。
DYNASCAL では、縦断的非対称関係行列のそれぞれに対して、まず Guttman (1968) の SSA-II を施し、各成員の2次元布置を得る。この布置は、隣接布置 ごとにプロクラステス回転により可能な限り近い布置になるように回転される。それ により得られた各観測時点での回転後の布置を、その後各成員ごとの1次元数列と みなし、まず1次元スプラインにより平滑化する。つぎに2次元スプラインにより、 各時点の布置を平滑化すると同時に、各時点の格子点上でのスプライン関数の微係数 を計算し、各時点ごと各格子点ごとのベクトルの推定値とする。それらが得られたら、 各時点ごと、一般の非線形線形微分方程式系を仮定し、各時点の系を(本来は 非自励系 (nonautonomous system) であるが) 自励系 (autonomous system) とみなし、各時点のベクトル場の特異点とそれらから出入りする幾つかの解軌道を 数値積分により計算し出力する。
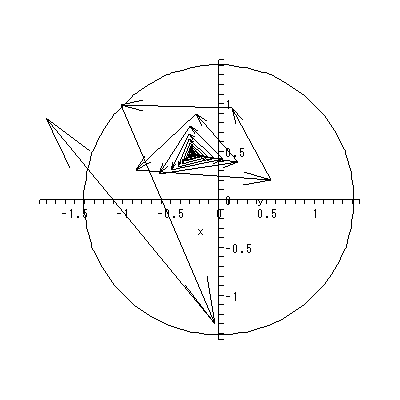
図 1.20 は、そのような推定されたベクトル場とその特異点および一部の解軌道 の出力結果の架空の例による図である。この例では、ベクトル場には、2つの渦状 沈点と2つの鞍点がある。
DYNASCAL では、このような場が時間と共にダイナミックに変化していく場とそ の特徴をコンピュータにより描き出すが、注意すべき点が1つある。それは、 DYNASCAL では、そのアルゴリズムから、もともと (1.40) 式のような自励系ではな く、2次元ベクトル x および時間 t を用いて、
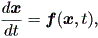
| (1.83) |
なる非自励系をデータにフィットさせているに過ぎない。したがって、各時点の2次元 ベクトル場で微係数ゼロの点を特異点として推定しているが、3次元的にみると正確に は
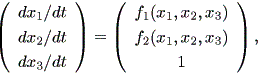
| (1.84) |
となっている、すなわちこのような系では、3次元目の微係数は常に1であり、ゼロに はならない。
この性質は、DYNASCAL では、本来 (1.80) 式で仮定されるべき何らかの分岐パラ メータ(複数) c をすべて時間軸上に投影されたものとみなしていると言える。
いずれにせよ、DYNASCAL は、縦断的非対称関係行列から、成員の対人的相互作用に より生じるであろう心理学的力の場とその特徴をわかりやすく描き出す方法であるが、 問題点もなきにしもあらずである。それらは、つぎのような点である(千野、2003b):
|
また、DYNASCAL は、一種の帰納的モデルであり、当該現象についての複数の公理的 言明から導かれる演繹的モデルではないので、多くの統計的モデルと同様、得られた 結果は事後的な解釈の域を出ない。
このような問題点を克服する1つの方法は、微分方程式ではなく、差分方程式 を用い、少数個の公理的言明から出発する演繹的モデルを構成することであろう。
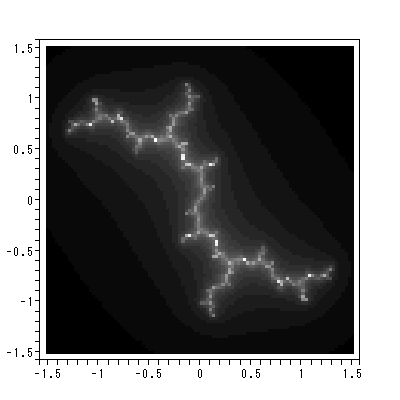
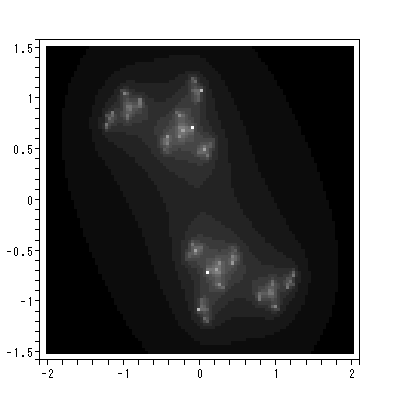
ここでは、著名な Newcomb (1961) の縦断的親近度データに対する Chino and Nakagawa (1990) による DYNASCAL の適用例を紹介する。ニューカムは、お互いに見ず知らずの 17名の学生をある寮で生活させ、16週にわたり彼らを観察し、彼らに対して自分を 除く16名の成員に対する魅力の程度を完全順位法で評定させた。データは1年目と 2年目の二組あるが、ここでは2年目の実験における0週目から15週目までのソシオ マトリックスを用いた。データの一部は、千野ホームページ上の付表 1.1 に示す。
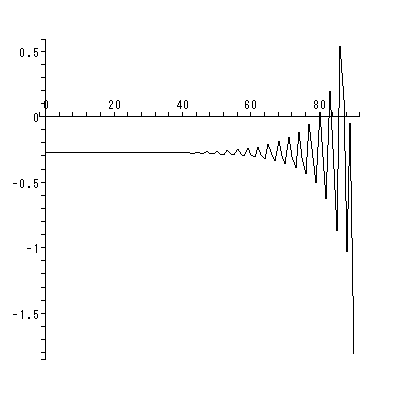
同じくホームページ上の付図 1.1 から付図 1.3 は、DYNASCAL が描き出した第0、 1、15週のベクトル場と一部の解軌道である。付図 1.1 の推定ベクトル場からは、 0週目では心理学的空間は、中央上部の鞍点により2領域に分割されているこ とや、第3象限のオメガリミットサイクルからは、一旦形成されかかった下位集団 の芽が既につぶれつつある状況が読み取れる。ソシオグラムでは、この領域には、 成員1、6、8、13から成る下位集団が対応する。また、これと対極にある第1お よび第4象限に位置する成員は、ソシオグラムでは、成員2、3、4、7、9、 11、12、17からなるグループが対応する。
1週目のベクトル場(付図 1.2) は、0週目と比べ様変わりしている。しかし、原点 近くの鞍点により大雑把には未だ集団はその左側の下位集団と同右側の下位集団 にわかれている。ただし、第4象限の渦状源点により、両グループの一部が混じ りあう方向に動いているように見える。
15週目のベクトル場(付図 1.3)では、寮でのグループ生活も最後になり、下位 集団も全体的に分解しつつあるように見える。
力学系を実際の問題に応用する場合には、単に系を記述したり、系の振る舞いを予測 したりするだけでなく、研究者が関心を持っている現象について、系を人為的に制御 したいであろう。これが可能になれば、心理学における力学系の理論も単なるお話で はなくなり、多くの現実の問題に役立つ。物理学や工学の世界では、このような考え 方はあたりまえであろうが、心理学や社会行動科学の分野では今後の取り組むべき 課題の1つであろう。
筆者は、現状ではこれらについては知識を持ち合わせていないが、興味がある読者は 例えば、以下のテキストが役立つのではなかろうか:
まず、古典的なテキストとしては厳密でかつわかりやすく書かれているのが Lefschetz (1965) である。この本は、加藤 (1974) による邦訳もある。この本には 非線形制御系の安定性に関する基礎的なことがらが議論されているので、一読すべき 本といえよう。
一方、カオスの制御については、例えばとっつきやすそうなものに Kapitaniak (1996) がある。また、多くの研究者によるカオス制御の理論と応用をまとめたもの として、例えば Schuster (1999) がある。
差分力学系について紹介し、筆者の最近関心を持って取り組みつつある複素(差分) 力学系における第2章との関連では、複素ヒルベルト空間や不定計量空間を状態変数 とするが、ヒルベルト空間上での系の制御に関しては、例えば Feintuch (1998) には、 ヒルベルト空間における制御理論が議論されている。
ここでは、各種差分方程式 (difference equation) とそのその解のうち、最も 単純なケース
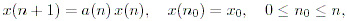
| (2.1) |
について述べる。この方程式は、線形斉次一次差分方程式 (a linear homogeneous first-order difference equation) と呼ばれる (例えば、Elaydi, 1999)。
この初期値問題の解は、
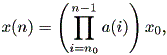
| (2.2) |
となる。
これに対して、

| (2.3) |
は、線形非斉次一次差分方程式 (a linear nonhomogeneous first-order difference equation) と呼ばれる。
この場合、解は、
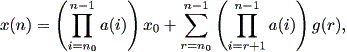
| (2.4) |
となる。
一方、差分方程式では、つぎの形の方程式を k - 次非斉次線形差分 方程式 と呼ぶ(Elaydi, 1999, p.54):
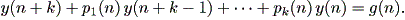
|
(2.3) 式で、特に a (n) = a かつ g (n) = b の場合は、
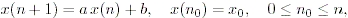
| (2.5) |
となり、その解は、
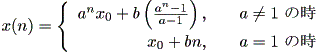
| (2.6) |
(2.6) 式で n → ∞ としたとき、解曲線はつぎのように分類できる:
|
微分方程式系の場合と同様に、状態空間が多次元(ここでは、 k 次元とする)の場 合の線形一次差分方程式の組は、 線形一次差分方程式系 (a system of linear first-order difference equations) と呼ばれ、つぎのように書かれる:
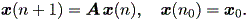
| (2.7) |
ここで、
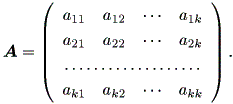
| (2.8) |
は、実正則行列 (real nonsingular matrix) とする。
(2.7) 式の解は、つぎのようになる:
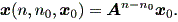
| (2.9) |
(註1) ここで、 y (n - n0) = x (n) とおけば、y (n+1) = A y (n) で、 y (0) = x (n0) なので、 (2.9) 式は一般性を失わず、
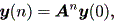
| (2.10) |
と書ける。
(註2) (2.7) 式の行列 A が与えられた時、 An を計算するには、 パッツァアルゴリズム (the Putzer algorithm) (例えば、Elaydi, 1999, p.106) を用いるとよい。
(註3) (2.7) 式で、 x(n) = ( x1(n), x2(n), ..., xk(n) )t が、 k 個の状態 (states) s1, s2, ..., sk の生起確率から成る、 すなわち、 x(n) = p(n) = ( p1(n), p2(n), ..., pk(n) )t であり、行列 A = P = { pij = p( si | sj ) }、すなわち、その要素 pij が現在の状態 sj がつぎの時点で si に移る確率であると仮定すると、
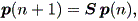
| (2.11) |
と書け、マルコフ連鎖 (the Markov chain) と呼ばれる。また、
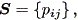
| (2.12) |
は、推移行列 (the transition matrix) と呼ばれる。
一般に、行列 A = { aij } は、 A のすべての要素に対して aij ≧ 0 ならば、非負と呼ばれる。もし、 k × k の非負行列 A が、すべての j = 1, 2, ...,k に対して ∑i=1k aij = 1 ならば、 マルコフ (Markov) または確率的 (stochastic) と呼ばれる。
一般に、マルコフ行列のすべての固有値 λ は、 | λ | ≦ 1 であることがわかっている(例えば、Elaydi, 1999, p.142)。また、マルコフ行列では λ = 1 は単根で、それ以外の根については | λ | ≦ ρ(A) であることもわかっている。 ρ(A) は、 k× k 行列のスペクトル 半径 (the spectral radius) すなわち、 ρ(A) = max1≦i≦k | λi | である (ペロンの定理 (the Perron's theorem)) (Elaydi, 1999, p.142)。
最初に、実差分方程式の平衡点およびその安定性の定義を行なう。
定義1 実非線形差分方程式
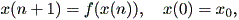
| (2.13) |
の点 x* は、もしそれが f の 固定点 (the fixed point) 、すなわち

| (2.14) |
であるならば、 (2.13) 式の 平衡点 (the equilibrium point) と呼ばれる。
(註1) (2.14) 式の固定点の定義は、微分方程式の固定点の定義式、すなわち第 1章の (1.7) 式に等しい。一方、差分方程式での平衡点は、微分方程式における微 係数(その点でのベクトル)にあたるものが x (n) における x(n+1) - x(n) と見な せるので、 (2.14) 式が成り立てば、 x(n+1) - x(n) = 0 、すなわち平衡点ということに なる。
定義2
|
(註1) 平衡点 x* が安定とは、簡潔に表現すれば、初期値 x0 が平衡点 x* から δ > 0 内にある時、どんな n > 0 に対しても、 xn は x* から ε > 0 の中にある場合をさす。したがって、必ずしも xn は x* に収束しなくてもよい。
(註2) 平衡点 x* が吸引的とは、初期値 x0 が平衡点 x* から η > 0 内にあれば、 xn が n → ∞ の時、平衡点 x* に収束する 場合をさす。一方、大局的吸引的とは、初期値 x0 が平衡点 x* から有限の 範囲にあればいつでも、 xn が n → ∞ の時、平衡点 x* に収束する 場合をさす。
(註3) 平衡点 x* が漸近安定とは、初期値 x0 が x* から η > 0 内にあれば、どんな n > 0 に対しても、 xn は x* から ε > 0 の中 にあり、かつ n → ∞ の時、平衡点 x* に収束する場合をさす。
ここでは、実非線形差分方程式の安定性の基準(例えば、Elaydi, 1999)について述 べる。
定理1 x* は実非線形差分方程式
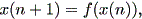
| (2.15) |
の平衡点であるとする。ここで、 f は x* で連続的に微分可能であるとする。この 時、
|
(註1) 差分力学系は、平衡点 x* は | f '(x*) | ≠ 1 の時、 双曲的 (hyperbolic) と呼ばれる。
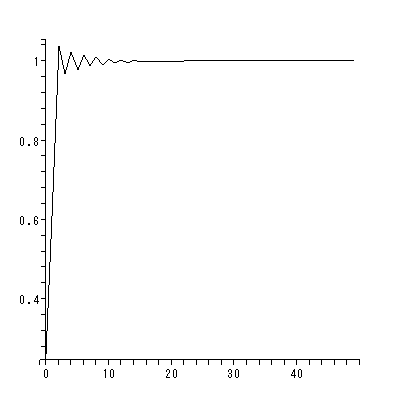
|
定理2 (2.15) 式の平衡点 x* に対して、 f ' (x*) = 1 とする。この時、
|
定理3 (2.15) 式の平衡点 x* に対して、 f '(x*) = - 1 とする。この時、
|
(註1) 一般に、 S f (x) は シュワルツの導関数 (the Schwarzian derivative of a function f) と呼ばれ、
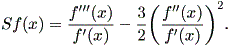
| (2.16) |
差分方程式では、平衡点以外に、ある正整数 k に対して、 k 回目ごとに同じ点 に戻る点、すなわち 周期点 (a periodic point) を考えることができる。正確 な定義はつぎのようである(Elaydi, 1999):
定義3 点 b は、 f の定義域内にあるとする。この時、
|
(註1) 上田ら (1995) は、うえの「k-周期」を「 b0 の周期系」と呼んでいる。
(註2) 宇敷訳 (1988, p.54) では、うえの「不測 k-周期的」を「終局周期的」と 訳している。
|
|
定義4 点 b は、 f の k-周期点とする。この時、点 b は
|
という。
定義4からは、もし点 b が安定性を持つならば、k-周期 { x(0) = b, x(1) = f(b) , ... , x(k-1) = f k-1 (b) } のどの点も安定性 を持つ、と言える。このことから、定理1は、k-周期点の安定性に関して、つぎの ように修正される:
定理4 O (b) = { b = x(0), x(1), ..., x(k-1) } は、連続 的微分可能な関数 f の k-周期(系)とする。この時、k-周期(系)は、もし
|
である。
|
微分方程式系 dx/dt = f (x,t,b) や dx/dt = f (x,b) に おけるパラメータ b の変化による特異点(固定点、浮動点など)の変化は、 第1章で見てきたが、これと同様、差分方程式系 x (n+1) = f (x (n),n,b) でも、固定点の近傍の系の振る舞いが b の変化により変わる様子は分岐理論が 扱う。
例えば、Peitgen and Richter (1986) には、よく知られたベリュルストー の力学 (Verhulst dynamics) が紹介されている。この系は、個体数の増殖モデル であり、ある時点でのある生物の個体数を x(0) とし、 n 年後の個体数を x(n) 、その生物の増殖率を R とする。フェアフルストは、 R = r (1-x(n)) と仮定した。こうすると、個体数の変化は、 x(n+1) = (1 + R) x(n) と書けるので、 個体数の変化の法則は、つぎの形となる:
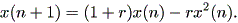
|
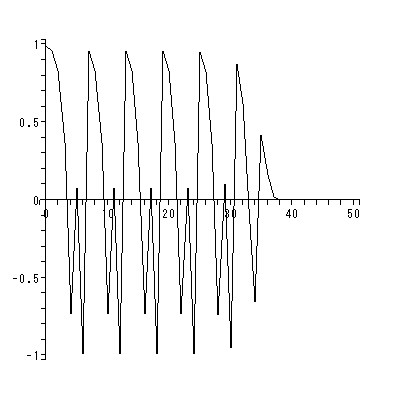
もちろん、この式における r は、分岐パラメータと見なせる。この式における r の値を変化させると、個体数の経年変化の仕方は r が ある値になると突然大きく変わる。また、 r がある値までは n をどんどん大き くしてやると、個体数はある値(図 2.1)あるいは複数の値(図 2.2、図 2.3)のいず れかに収束するが、 r がある特定の値を超えると、個体数の経年変化は(変化を表 す式が決定論的方程式であるにもかかわらず)まったくでたらめになり予測不可能と なる(図 2.4)、いわゆる、カオス (chaos) が現れる。ここで、これらの図で の初期値は x(0) = 0.1 とした。
このように、差分方程式では、微分方程式と異なり、一般に、実1変数差分方程式 でさえ、分岐を経由してカオスが現れる点が、大きな特徴である。
この節では、実数係数の非自励系差分方程式系の平衡点とその安定性について述べる。 まず、実係数非自励系差分方程式系の正確な定義は、つぎのようである:
定義5
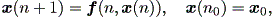
| (2.18) |
ここで、 x(n) ⊆ Rk、 f: z+ × Rk → Rk。また、 f(n,x(n)) は、 x で連続とする。 (2.18) 式は、 n が陽な形で入って おり、非自励系 (nonaoutonomous) である。 (2.18) 式で引数に陽に n が入らない 時、すなわち、 x(n+1) = f(x(n)) ならば、系は 自励系 (autonomous) である。一方、 (2.18) 式の系は、もし n ⊆ Z に対して、ある 正整数 N に対して

| (2.19) |
ならば、周期的 (periodic) と呼ばれる。
Rk 上の点 x* は、もし f(n, x*) = x* ならば、(すべての n ≧ n0 に対して)、 (2.18) 式の平衡点 (an equilibrium point) と呼ば れる。
(註1) 多くのの文献では、 x* は原点 0 と仮定される。その根拠は、 x* ≠ 0 に対して、 y(n) = x(n) - x* とすると、 (2.18) 式は
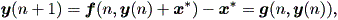
|
と書ける。また、y = 0 は x = x* に対応することに注意すればよい。
(註2) (2.18) 式の解の存在の証明は、例えば Elaydi (1999, p.157) にある。
定義6 (2.18) 式の平衡点 x* は、
|
最後に、うえの (ii) と (iii) で、 μ = ∞ あるいは (iv) で δ = ∞ ならば、当該安定性は 大局的 (global) と呼ばれる。
2.1.3 節では、一般の k -次元線形一次差分方程式系を紹介したが、ここでは、 その特別な場合である2次元自励系の振る舞いについて簡単に紹介する。
まず、前節での一般の平衡点の定義から、 x を2次ベクトル(2次元ベクトル) とする自励系

| (2.20) |
を考えよう。もちろん、この場合、係数行列 A は2次の実正方行列である。
前節での平衡点の定義から、 A x* = x*、すなわち
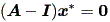
|
なる点が、 (2.20) 式の平衡点である。したがって、行列式 | A - I | ≠ 0 ならば、平衡点は x* = 0 である。
一方、行列式 | A - I | = 0 ならば、任意の点を c とすれば、 x* = c はすべて平衡点となる。しかし、この場合は、 y = x(n) - x* とおけば、 (2.20) 式は、 y(n+1) = A y(n) とできるので、 x* ≠ 0 のような平衡点の安定性の検討にも、 x* = 0 と仮定してよい。
一般に、 (2.20) 式における行列 A は、 x(n) = P y(n) (ここで、 P は正則とする)と変形すると、 (2.20) 式はつぎのようになる:
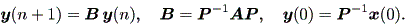
| (2.21) |
ここで、 y(0) = k = (k1, k2)t とする。
うえの結果から、 (1.1.2) 節の微分方程式系の場合と同様、 A の実標準形 B は、 (1.1.2) 節で述べた次数2の場合の3種類、すなわち (a)、 (b)、 (c) のいずれかとなる。
Case (a) 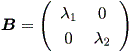
この時、 (2.21) 式は、
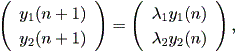
| (2.22) |
となり、各次元ごと、1次元線形差分方程式の解、すなわち (2.6) 式で b = 0 より、
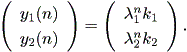
| (2.23) |
(2.23) 式より、
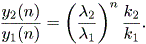
| (2.24) |
(2.23)、 (2.24) 式より、まず λ1 ≠ λ2 の場合、固定点の近傍で の解軌道の特徴は、 λ11、 λ2 の値に応じて、サドル (saddle) 、漸近的安定ノード (asymptotically stable node)、または 不安定ノード (unstable node) となる。
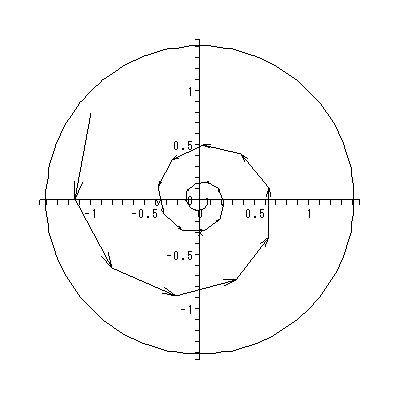
|
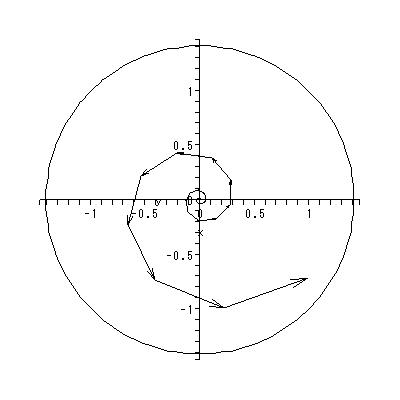
|
ここで、差分系の場合、微分系と大きく異なるのは、微分系では軌道特性を大きく 変える固有値の値がゼロであるのに対して、それが1である点であることに注意が必要 である。この違いは、明らかに微分系では解曲線(軌道)の基本が、既に見たように、 固有値の指数関数 になるのに対して、 差分系では 固有値のべき関数になる点に起因する。
|

|
Case (b)
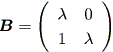
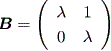
まず、
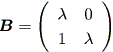
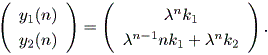
| (2.25) |
一方、
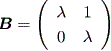
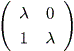
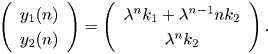
| (2.26) |
|
|
結局、上記2つの系の軌道特性は、微分力学系での図 1.10 や図 1.11の内向き仮性 結節点に似通ったものとなる。それらは、差分系では漸近的安定結節点 (asymptotically stable node) と呼ばれる (Elaydi, 1999)。これらの場合、 0 < λ <1 である。 これに対して、 λ > 1 の場合は、微分力学系での図 1.12 や図 1.13 の外向き仮性結節点に似通ったものとなる。
Case (c)
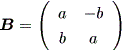
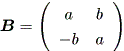
まず、
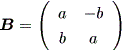
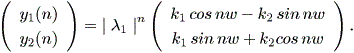
| (2.27) |
図 2.5 は、固有値 λ が共役根を持ち、その絶対値が1より小さいケース の1つであり、この場合渦状沈点となる。
一方、図 2.6 は、固有値が同じく共役根を持ち、その絶対値が1より大きいケー スの1つであり、渦状源点となる。
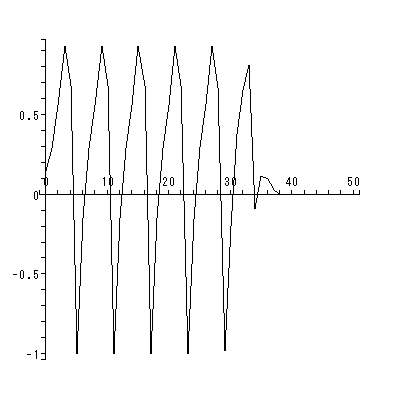
|
アレクサンダーによれば、この時期にまずドイツの数学者シュレーダーとイギリス の数学者ケイリーがいわゆるニュートン法の(複素2次関数に関する)複素根への 収束の研究を行なっている (Cayley, 1879; Schroder, 1870, 1871)。つぎに簡単に 紹介する複素力学系の基本的概念である ジュリア集合 (the Julia set)、お よび 充填ジュリア集合 (the filled Julia set)、及び ファトウ集合 (the Fatou set) は、シュレーダーらの 研究から4、50年後にフランスの数学者であるファトウとジュリアによる。
このように、複素力学系の研究は100年以上も前から研究されて来ているが、 未だわからない問題もたくさんあり、現在もまだアクティブな研究領域であるという。
この節では、ジュリア集合、充填ジュリア集合、及びファトウ集合の定義を、 上田にしたがって行なう(上田ら、1995)。
|
まず、 f (z) は複素変数を定義域とする p ≧ 2 なる複素多項式
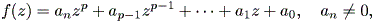
| (2.28) |
とする。
定義7
|
(2.28) 式で、 p = 2 の特別なケース
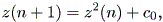
| (2.29) |
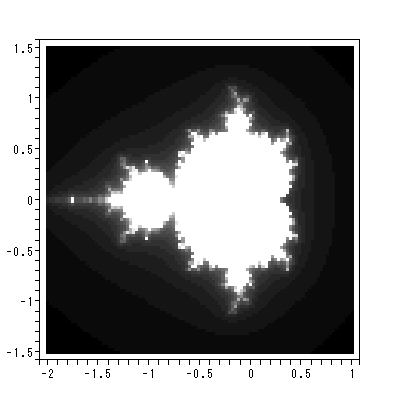
について、実軸及び虚軸のある範囲の格子点の値を c0 として、軌道が有界な 集合をプロットしたものは、マンデルブロー集合 (the Mandelbrot set) として知られている。図 2.12 は、これを示す。
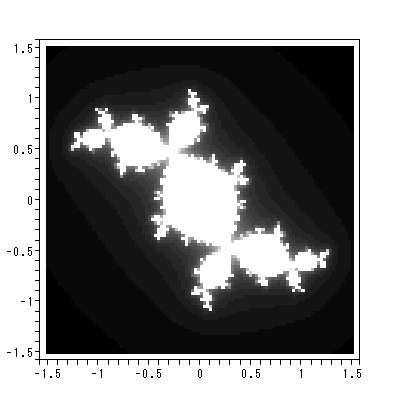
|
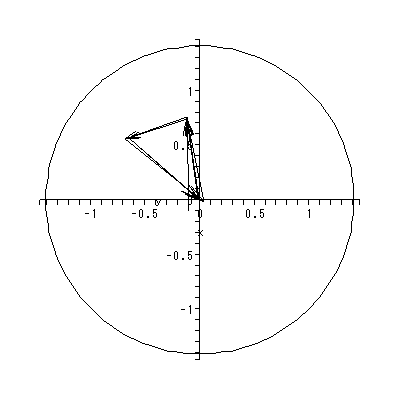
|
例1
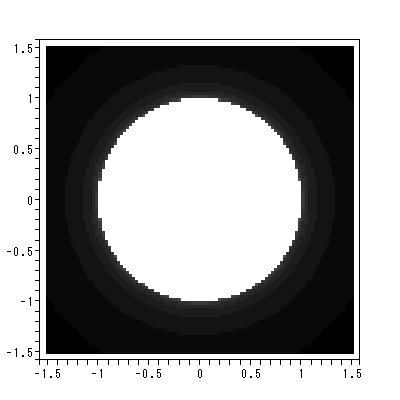
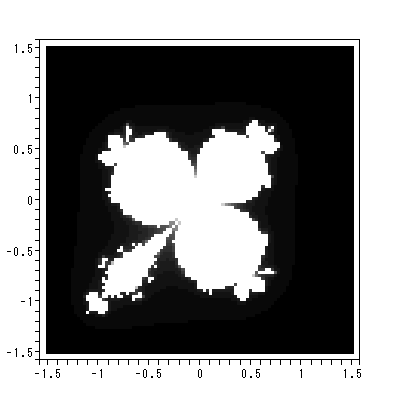
図 2.7 は、上田ら (1995) にあげられている最も単純なジュリア集合の場合を Maple に描かせたものである。系の方程式は、きわめて単純で、マンデルブローの力 学系において、 c0 = 0 のケースである。図中、白と黒の境界は、メッシュの粗さか ら、少しぎざぎざした円に近いものが見えるが、理論的には完全な円であり、これが この系のジュリア集合である。円及び円の内部を合わせたものが充填ジュリア集合で ある。充填ジュリア集合からジュリア集合(この例では円)を除いた部分は、この例 でのファトウ集合である。
このような単純な系でさえ、充填ジュリア集合内での系の振舞いは多様である。 例えば、図 2.8 は、この系での円の内部の1点を初期値とした時の反復13回の軌道 を描いたものである。実軸、虚軸ごとの動きを描いてみると、この場合、6回目ぐらい で既にほとんど原点に達していることがわかる。この系の固定点は z2 = z から容易 に計算できて、0と1であることがわかる。また、固定点の安定性の議論から、前者は 超吸引的、後者は反発的であることがわかる。つまり、前者の軌道は図にも見られる ように、時間と共に次第に原点に引き寄せられる。
|
|
一方、図 2.9 のように円周上のある点から出発した場合、図 2.10 および図 2.11 の実軸及び虚軸上の軌道を見ると、20数回の反復までは周期的動きをするが、その あとは次第に原点に引き寄せられていくことがわかる。実は、理論上はこの場合は円 周上を無限に動き、カオスとなるはずであるが、この例のように計算機の丸めの誤差 により、一見カオスでないように振舞うのである。この例の場合、たまたまある反復 で、円内に落ちたが、逆に計算誤差により円外に落ちる場合もあるはずである。
一般に、構造不安定な系の振る舞いやこの場合のカオスのような場合、誤差を伴う 如何なる観測でも、そこでの真の振る舞いは捕らえることができず、そのような場合、 観測データに対する統計的なモデルのフィットそのものが無意味になる。そのような 時には、どうしても理論的モデルないしはメタモデルのレベルでの数学的な検討が不 可欠である。
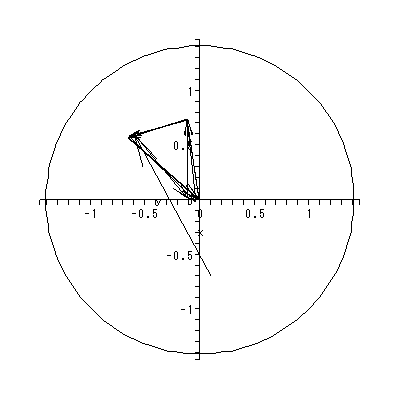
|
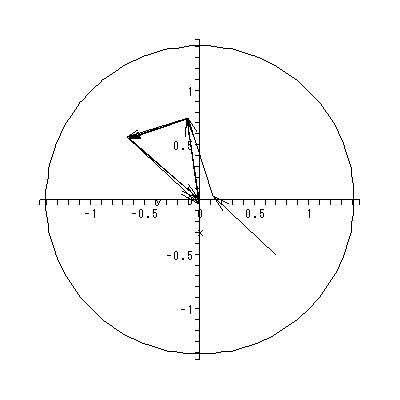
|
例2
図 2.13 は、Peitgen and Richter (1986) の本文中の fig.4 を Maple で描かせたものである。この系は、マンデルブローの力学系において、 c0 = -0.12+0.74i のケースである。この系の固定点は、 1.2737-0.4782i および -0.2737+0.4782i の近くに位置し、共に反発的固定点である。特に後者の固定点は、 図中の主要な5枚の葉のうちの第2象限に位置する2枚と原点に中心があり4象限 にまたがる最大の葉がつながる根元に位置する。さらに、この系には、これら3枚 の葉の中心にある3周期点を特徴とする。
この系の充填ジュリア集合は図中の白い部分全体であり、黒い部分との境目の集合が ジュリア集合である。ジュリア集合は、この場合、図 2.7 の系の場合のそれのような 単純な円ではなく、Peitgen and Richter の言葉では無限個のゆがんだ円周 (an infinite number of deformed circles) から成る。
この系で、原点が中心にある最大の葉の中心近くから出発した軌道を描いたのが図 2.14 である。この場合、3周期点を反時計回りで回る周期軌道が現れていることが わかる。
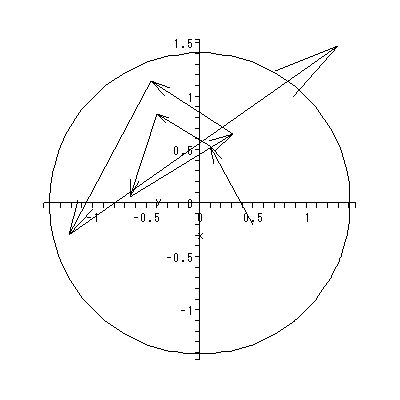
|
|
一方、この系の主要な5つの葉のうちの上側3つの中心にある反発的固定点のすぐ 近くを初期点とした場合、反発的周期点の性質から予想されるように、図 2.15 から、 軌道は最初は固定点の近くでほとんど動かないが、次第に固定点から離れ、ある反復 の後には、この系のジュリア集合からどんどん離れていくことがわかる。図 2.16 は、 この点を見やすくするために、図 2.15 の複素平面状での軌道のうち、実軸上の動き のみを示したものである。図には示していないが、もちろん虚軸の動きも同様な特徴 が見られる。
初期点がこの系の第4象限にある2つの主要な葉にある場合、どうなるであろうか。 図 2.17 及び図 2.18 は、それぞれ初期点を 0.1 - 0.7i 及び 0.7 - 0.5i とした場合 の軌道を示す。第4象限の2つの主要な葉のうち左側のそれから出発する前者の場合に は、図 2.17 から明らかなように、軌道は最初原点に中心を持つ最大の葉には入らず、 第2象限の2つの主要な葉のうちの左側の内部の周期点の1つに入り、その直後に最大 の葉に入り、その後は反時計回りで3周期点を回り続ける。
|
|
一方、図 2.18 から明らかなように、第4象限の2つの主要な葉の右側から出発する 場合は、最初原点に中心を持つ最大の葉に入り、その後、反時計まわりで3周期点を回 り続ける。
最後に、第1象限の充填ジュリア集合の少し外側の点 0.5-0.2i から出発する場合 の軌道を示したのが図 2.19 である。この場合、軌道はこの系の充填ジュリア集合の 外側を迂回しながら、徐々にそれを離れていくことがわかる。
例3
マンデルブローの力学系は、 c0 = i の場合、Peitogen and Richter (1986) の本文 中の図 12 にあるような樹状枝となる。図 2.20 は、これを Maple に描かせたもの である。この系での充填ジュリア集合は、内点を持たず、それ自身がジュリア集合と なっている。この系は固定点として、 z = 1.3002 - 0.6248i 及び z = - 0.3002 + 0.6248i の近くの値を持つ。共に、反発的である。実際、後者の固定点の近傍を初期点とした 時の軌道を描かせると図 2.21 のようになり、そのことが確認できる。
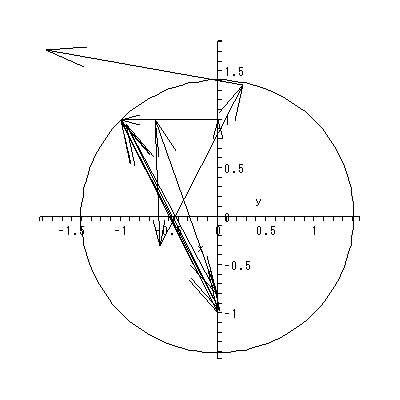
|
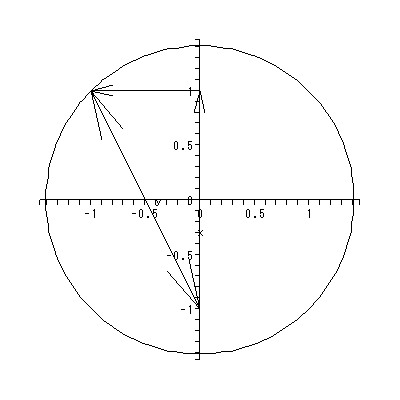
|
一方、この系には2周期点も存在することが計算からわかる。実際、2周期点は、 z = - 1 + i 及び - i である。例えば、樹状枝上の1点 i から出発する軌道を描かせ てみると図 2.22 のようになり、1回の反復で2周期点のうちの1つの z = - 1 + i に 入り、その後は他方の周期点 z = - i との間を永久に行き来する周期軌道となる。
それに対して、樹状枝上の原点よりわずかにずれた点 ( z = 0.001 + 0.001 i ) から出 発する軌道は、30回の反復のうち、最初の反復で2周期点の近くを往復する周期軌 道が8回ほどの反復後ブレだし、次第に無限遠点に向かう(図 2.23)。同じく、樹 状枝上に位置するもう1つの出発点 z = 0 (すなわち原点)から始まる軌道では、2 回の反復で2周期点間を往復する周期軌道となる(図 2.24)。図 2.25 は、この軌 道の実軸のみの値の変動を30回の反復までプロットしたものである。
|
|
例4
図 2.26 は、Peitgen and Richter (1986) の本文中の fig.11 に掲載されている図と 同種の系(ファトウの塵 (Fatou dust))をMaple で描いたものである。この系は マンデルブロー集合の外で当該集合に近い c0 の値、ここでは例3の系に近いマン デルブロー集合の外の c0 = 0.2 + i の場合の系である。
図からも推察されるように、このような場合、ジュリア集合はばらばらになって雲の ような塵状の集合になる。アトラクタは、この場合無限遠点のみである。図 2.27 は、 図 2.26 の右下の比較的雲の多い部分と見なされる点 z = 0.2 - 0.7 i から出発した軌道 を示す。また、図 2.28 は、図 2.27 の場合より右下の z = 1.2 - i から出発した軌道を 示す。この場合、さらに早い段階で無限遠点に向かう。
千野(Chino, 2000; 2002; 2003a; 千野、2003b; Chino, 2004) は、最近非対称 MDS の1つである HFM を応用して、対人相互作用の複素差分方程式モデルを提案してい るが、モデル自身の状態空間がもともと複素空間であるので、自然に複素力学系が導 かれる。このモデルにおける状態空間は、(有限次元)複素ヒルベルト空間 (finite-dimensional Hilbert space) もしくは不定計量空間 (indefinite metric space) である。その理由は、各時点での成員相互の非対称な関係から成員の 遠近関係をコンパクトに表現することを考えると、1つのやり方はそのような空間を 考えることであり、非対称 MDS からの1つの帰結なのである (Chino, 1998; Chino & Shiraiwa, 1993)。
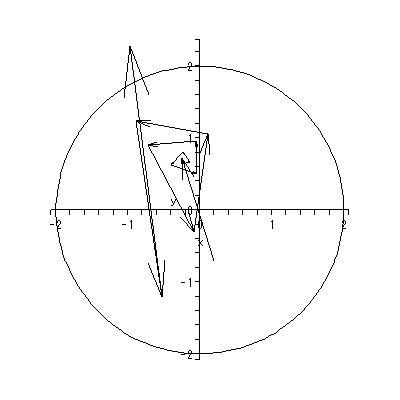
|
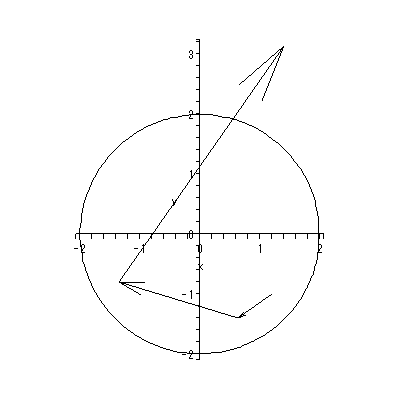
|
まず、Chino (2000) のモデルでは、DYNASCAL と異なり、対人相互作用に関して、 以下の心理学的仮定を置く:
|
前節の3つの基本的仮定のもとで、以下に述べるような単純な線形モデルや非線形 モデル等を考えることができよう (Chino, 2000)。まず、単純線形モデル (a simple linear model)は、つぎのように書けよう:
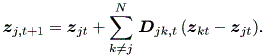
| (2.30) |
ここで、 Djk,t = diag { wjk,t(1) , ・・・ , wjk,t(p) } , であり j = 1, 2, ・・・, N である。また、
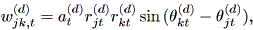
| (2.31) |
であり、 d = 1, 2, ・・・, p である。
このモデルで、 zjt は成員 Oj の第 t 時点での(多次元)複素空間 上の位置を表す。このモデルで、複素第 d 次元の2名の成員相互の動きを図示する と図 2.29 のようになる (Chino, 2002, fig.1)。
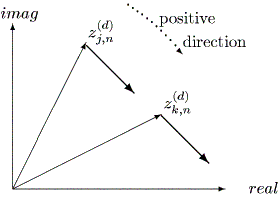
|
これに対して、一般非線形モデル (a general nonlinear model) としては、
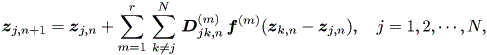
| (2.32) |
ここで、
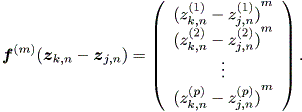
| (2.33) |
さらに、 Djk,n(m) = diag { wjk,n(1,m) , ・・・ , wjk,n(p,m) } , そして
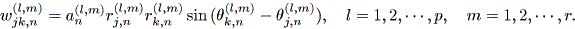
| (2.34) |
つぎに上記モデルによる成員の動きについて、複素力学系の理論を応用する 可能性について若干ふれる。例えば、うえの一般の非線形系 (2.32) 式のモデルで、 次元数は1、モデルの次数 m は2、かつ成員数は2であるとしよう。この場合、 成員 j 及び成員 k の時点 n での座標値を順に zjn、 zkn と書けば、 (2.32) 式はつぎのように書ける:
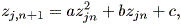
| (2.35) |
ここで、
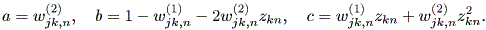
| (2.36) |
|
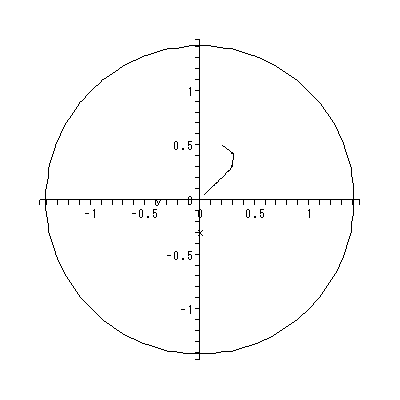
|
この式から、もし成員 j が成員 k との心理的距離を無視して(異常な)行動を 起こすとすれば、(この系は原点を移動すれば、明らかに (2.29) 式で表されるマン デルブロー集合に等しいので)成員 j の動きには既述の例1から例4などの多く のケースがあり得ることになる。
成員数を3以上にした場合も、同様な考察を行うことができる。例えば、 (2.32) 式で、空間の次元数 p = 1 で、関数 f の次数 m = 2 、かつ成員数が一般の N の 場合は、 (2.35) 式の2次式の係数は、
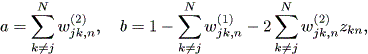
| (2.37) |
及び

| (2.38) |
となる。この系も、上記の系と同様、マンデルブロー集合となる。
|
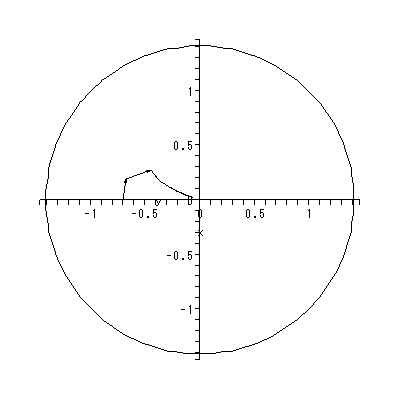
|
より一般的なケースとして、 p = 1 で関数 f の次数 m = r の時は、 (2.32) 式 は
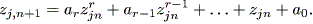
| (2.39) |
ここで、
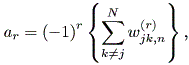
| (2.40) |
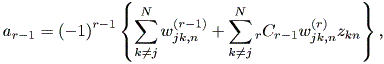
| (2.41) |

| (2.42) |
及び
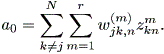
| (2.43) |
となる。 (2.39) 式は、マンデルブロー集合をその特殊ケースとして含む、より一般的な 集合である。このような集合では、さらにいろいろな動きが含まれる。
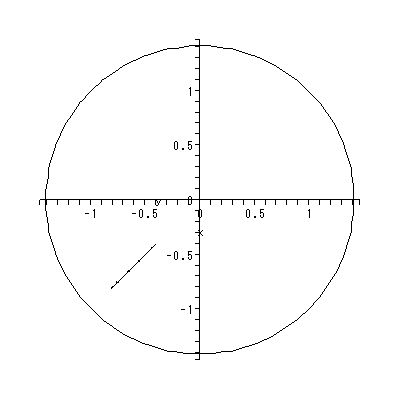
|
例えば、 (2.39) 式で r = 5 の例として、Milnor (2000) の fig.15 をあげる。 このジュリア集合は、差分方程式
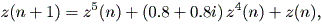
| (2.44) |
から得られるものである。
この式から、まず固定点は2つあり、 z = 0 及び z = - 0.8 - 0.8 i であることを容易 に示すことができる。さらに、固有値の特徴から、前者はいわゆる中立固定点 (indifferent fixed point) であり、かつ放物的 (parabolic) であることもわ かる。一方、後者の固定点は、固有値の特徴から、吸引的であることがわかる。図 2.30 は、Milnor の fig.15 の代わりを Maple に描かせたものである。この図は、解像度が それほどよくないので、ギザギザの多くは形の崩れた円が無数にくっついているよう には見えないが、Milnor の図ではそれがよくわかるように描かれている。とりわけ、 前者の固定点、すなわち原点の放物的固定点を中心に持つ大きな3つのペダル (petal) は、相互に境界は原点のところまで延びているのだが、やはりこの図では解 像度が悪くそう見えないので注意されたい。
図 2.31 は、図 2.30 の系で、第1象限のペダルの内部から出発した時の軌道を 示す。一方、図 2.32 はその軌道の実軸の値のみ1000回の反復による変化を 描いたものである。これらの図から明らかなように、第1象限のペダルの内部から 出発する軌道は、原点の固定点に対してきわめてゆっくりと近づいていくことが わかる。
同様な軌道を、第2象限の大きなペダルの中心からやや下を初期点とした場合 が、図 2.33 である。この場合も、第1象限から出発した軌道と同様、原点の固定点 に対して、きわめてゆっくり近づいていく。
最後の図 2.34 は、原点から第3象限へ斜め左下の方向へ延びているイカの胴体 のような集合の中にあるこの系のもう1つの固定点の近くでの軌道の特徴を描いた ものである。この場合の軌道の初期点は、 z = - 0.9 - 0.85i とした。この時、軌道は 数回の反復でほぼ吸引的固定点 z = - 0.8 - 0.8i に達する。
(2.32) 式のモデルは、これらを複素次元1の特殊ケースとして含む複素多次元差分 力学系であるので、少なくとも理論的には無限に近い軌道特性を持つであろう。
前節では、一般非線形複素差分系 (2.32) 式の特別なケースについてのメタモデル の振る舞いについて検討したが、そのようなケースはあまり現実的ではない。メタ モデルレベルでの系の振る舞いの検討の中心は、もちろん、もとの線形複素差分系 (2.30) 式や一般非線形複素差分系 (2.32) 式のそれらである。

|
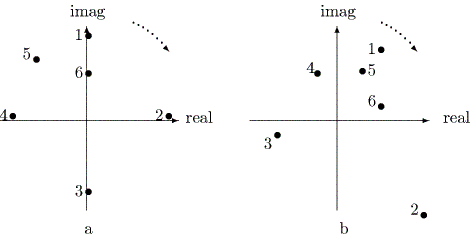
|
Chino (2000, 2003a) は、前者の線形複素差分系で状態空間が複素1次元の場合の 検討を行なっている。表 2.1 は、Chino (1978) の6名の成員間の架空の親近度データ であり、図 2.35a はこのデータに関する Chino and Shiraiwa (1993) によるエルミ ート形式モデル (Hermitian Form Model) の複素一次元解を示す。一方、図 2.35b は、筆者の線形複素差分系モデルでの8回の反復後の6名の成員の布置を示す。
この種のシミュレーションを線形、非線形の場合、さらには高次元の場合にも行なう ことにより、これらのモデルが妥当であると仮定した場合に起こりうる各種の系の 振る舞いが明らかになろう。これらについては、今後の検討課題の1つである。
これまでの議論は、メタモデル (a meta-model) のレベルの議論に過ぎない。 この種のモデルの妥当性は、縦断的ソシオマトリックスを収集し、適切な方法によ りモデルパラメータを推定することによりデータにフィットするかどうかを検討して 初めて検証できるものである。この点に関しては、筆者は昨年イタリアの国際計量心 理学会でモデルのパラメータの推定方法を幾つか発表したが (Chino, 2003a)、未だ 未完成であり、今後の課題である。
Alexander, D. S. (1994). A History of Complex Dynammics from Schroder to Fatou and Julia. Wiesbaden: Vieweg.
Amari, S. (1972). Characteristics of random nets of analog neuron-like elements. IEEE Transactions, SMC-2, 643-657.
Andronov, A. A., & Pontrjagin, L. S. (1937). Syst'emes grossiers. Doklady Akademii Nauk SSSR, 14, 247-250.
青木統夫・白岩謙一 (1985). 力学系とエントロピー 共立出版
Beardon, A. F. (2000). Iteration of Rational Functions. New York: Springer.
Cayley, A. (1879). Applications of the Newton-Fourier method to an imaginary root of an equation. Quarterly Journal of Pure and Applied Mathematics, 16, 179-185.
Chino, N. (1978). A graphical technique for representing the asymmetric relationships between N objects. Behaviormetrika, 5, 23-40.
Chino, N. (1987). A bifurcation model of changes in interdependence structure among objects. Bulletin of The Faculty of Humanities of Aichigakuin University, 17, 85-109.
千野直仁 (1991). 集団のシステム解析 三隅二不二・木下冨雄編 「現代社会心理学の発展 II」 第6章 数理モデル 2 (pp.385-413) ナカニシヤ出版
千野直仁 (1997). 非対称多次元尺度構成法 現代数学社
Chino, N. (1998). Hilbert space theory in psychology (1) - Basic concepts and possible applications. Bulletin of The Faculty of Letters of Aichi Gakuin University, 28, 45-65.
Chino, N. (2000). Complex difference system models of social interaction - Preliminary considerations and a simulation study. Bulletin of the Faculty of Letters of Aichi Gakuin University. 30, 43-54.
Chino, N. (2002). Complex space models for the analysis of asymmetry. In S. Nishisato, Y. Baba, H. Bozdogan, & K. Kanefuji (Eds.) Measurement and Multivariate Analysis, Tokyo: Springer. pp.107-114.
Chino, N. (2003a). Complex difference system models for the analysis of asymetry. In H. Yanai, A. Okada, K. Shigemasu, Y. Kano, & J. J. Meulman (Eds.) New Developments in Psychometrics, Tokyo: Springer. pp.479-486.
千野直仁 (2003b). 複素力学系による小集団の分析ー計量から理論・予測に向けて 科研シンポジウム「数理統計学と計量心理学をつなぐ」(研究代表者 赤平昌文) 予稿集 大阪
Chino, N. (2004). Behaviors of members predicted by a special case of a complex difference system model. Proceedings of the 32th annual meeting of the Behaviormetric Society of Japan, Yokohama, Japan.
Chino, N., & Nakagawa, M. (1983). A vector field model for sociometric data. Proceedings of the 11th annual meeting of the Behaviormetric Society of Japan (pp.9-10), Kyoto, September.
Chino, N., & Nakagawa, M. (1990). A bifurcation model of change in group structure. The Japanese Journal of Experimental Social Psychology, 29, No.3, 25-38.
Chino, N., & Shiraiwa, K. (1993). Geometrical structures of some non-distance models for asymmetric MDS. Behaviormetrika, 20, 35-47.
Duffing, G. (1918). Erzwungene Schwingungen bei Ver"anderlicher Eigenfrequenz. Vieweg: Braunschweig.
Eigen, M. , & Schuster, P. (1977a). The hypercycle-a principle of natural self-organization. Part A: Emergence of the hypercycle. Naturwiss., 64, 541-565.
Eigen, M. , & Schuster, P. (1977b). The hypercycle-a principle of natural self-organization. Part B: The abstract hypercycle. Naturwiss., 64,541-565.
Eigen, M. , & Schuster, P. (1977c). The hypercycle-a principle of natural self-organization. Part C: the realistic hypercycle. Naturwiss., 64, 541-565.
Elaydi, S. N. (1999). An introduction to differential equations. 2nd Ed., New York: Springer-Verlag.
Fentuch, A. (1998). Robust Control Theory in Hilbert Space. New York: Springer.
Guckenheimer, J. & Holmes, P. (1983). Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields. Berlin: Springer-Verlag.
Guttman, L. (1968). A general nonmetric technique for finding the smallest coordinate space for a configuration of points. Psychometrika, 33, 469-506.
Guttman, L., & Lingoes, J. C. (1973). The Guttman-Lingoes nonmetric program series, Ann Arbor: Mathesis Press.
Hartman, P. (1982). Ordinary Differential Equations, Second Edition, Boston: Birkh"auser.
Heath, R. A. (2000). Nonlinear Dynamics - Techniques and Applications in Psychology. London: Lawrence Erlbaum Associates.
Hirsch, M. W., & Smale, S. (1974). Differential equations, dynamical systems, and linear algebra. New York: Academic Press.
Hoppensteadt, F. (1993). Analysis and Simulation of Chaotic Systems. New York: Springer-Verlag.
Kapitaniak, T. (1996). Controlling Chaos. New York: Academic Press.
Lefschetz, S. (1965). Stability of Nonlinear Control Systems. New York: Academic Press.
レフシッツ S. 著 加藤順二訳 (1974). 非線形制御系の安定性 産業図書
Lewin, K. (1933). Environmental forces. In C. Murchison (Ed.) A Handbook of Child Psychology, Vol. 2, New York: Russell & Russell. pp.590-625.
Lewin, K., Birenbaum, G. (1930). Investigations of the psychology of action and affection. VIII. Forgetting an intention. Isolated psychic systems and dynamic total spheres. [Untersuchungen zur Handlungs- und Affektpsychologie. VIII. Das Vergessen einer Vornahme. Isolierte seelische Systeme und dynamische Gesamtbereiche.] Psychologische Forschung, 13, 218-285.
Milnor, J. (2000). Dynamics in One Complex Variable. 2nd edition. Wiesbaden:Vieweg & Sohn.
中野馨編著 (1990). ニューロコンピュータの基礎 コロナ社
Newcomb, T. M. (1961). The acquaintance process. New York: Holt. Rinehart and Winston.
Nourrit, D., Deligni`eres, D., Caillou, N., Deschamps, T., and Lauriot, B. (2003). On discontinuities in motor learning: A longitudinal study of complex skill acquisition on a ski-simulator. Journal of Motor Behavior, 35, 151-170.
Peitgen, H.-O., & Richter, P. H. (1986). The Beauty of Fractals. New York: Springer-Verlag.
パイトゲン H.-O ・リヒター P. H. (1986). フラクタルの美 宇敷重弘(訳) (1988). フラクタルの美 - 複素力学系のイメージ シュプリンガー・フェアラ ーク東京(株)
Rashevsky, N. (1940). An approach to the mathematical biophysics of Biological self-regulation and of cell polarity. Bulletin of Mathematical Biophysics, 2, 15-25.
Rayleigh, J. W. S. (1896). The Theory of Sound. Reprinted by Dover: New York.
Rosen, R. (1970). Dynamical System Theory in Biology, New York: Wiley-Interscience.
Rowe, G. W. (1994). Theoretical models in biology -The origin of life, the immune system, and the brain. Oxford: Clarendon.
Schr"oder, E. (1870). Ueber unendlich viele Algorithmen zur Aufl"osung der Gleichungen. Mathematische Annalen, 2, 317-365.
Schr"oder, E. (1871). Ueber iterite Functionen. Mathematische Annalen, 3, 296-322.
Schuster, H. G. (ed.) (1999). Handbook of Chaos Control. New York: Wiley-VCH.
白岩謙一 (1974). 力学系の理論 岩波書店
Sprott, J. C. (2003). Chaos and Time-Series Analysis. Oxford: Oxford University Press.
Tobler, W. (1976-77). Spatial interaction patterns. Journal of Environmental Systems, 6, 271-301.
Thompson, J. M. T., & Stewart, H. B. (1986). Nonlinear Dynamics and Chaos. New York: Wiley.
Tonge, D. G. (1974). Logical properties of the perceived behaviour patterns of a dynamical system. International Journal of Man-Machine Studies, 6, 715-728.
Tsuda, I. (1991). Chaotic neural networks and thesaurus. In A. V. Holden & Kryukov, V. I. (Eds.), Neurocomputers and attention, Chap. 2. Synchronization & Chaos: Vol.1. Neurobiology, Synchronisation and Chaos (pp.405-424). Manchester: Manchester University Press.
Turing, A. M. (1952). The chemical basis of morphogenesis. Philosophical Transactions of Royal Society, B237, 5-72.
上田哲生・谷口雅彦・諸澤俊介 (1995). 複素力学系序説 培風館
van der Pol, B. (1927). Forced oscillations in a circuit with nonlinear resistance (receptance with reactive triode). London, Edinburgh and Dublin Philosophical Magagine and Journal of Science, 3, 65-80.
Waddington, C. H. (1957). The Strategy of the Genes, London: George Allen & Unwin.
Yadohisa, H., & Niki, N. (1999). Vector field representation of asymmetric proximity data. Communications in Statistics, 28, 35-48.
ここでは、第1章 微分力学系における演習問題の証明を行なう。
演習 1.1 (単純な線形一次微分方程式の解の一意性の証明)
(証明) g (t) が任意の(他の)解として、
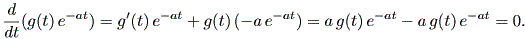
| (A.1) |
そこで、 g (t) e-at は定数(例えば、 k )である。そこで、 g (t) = eatk である。
演習 1.2 (線形一次微分方程式系の座標変換による系の変形の証明)
(証明) dx / dt = A x に対して座標変換 x = P y ( P は正則)を施せば、 dx / dt = d (Py) / dt = P dy / dt な ので、 dx / dt = P dy / dt = A (P y) 。そこで、 d y / dt = P-1 A P y と書ける。