このページは、令和2年4月27日に一部更新しました。
![]()
ここでは、反復測度 SPF_p.q デザイン ANOVA データの SAS による分散分 析を以下の2つのセクションに分けて示す。ただし、後者の出力結果のセクションの 一部にダウンロードコーナーの 2. 及び 3. の小さなプログラムを含めた。:
| 1.7.5.1 SAS による反復測度 SPF_p.q デザイン ANOVA プログラ ムとその概要 |
| 1.7.5.2 SAS による反復測度 SPF_p.q デザイン ANOVA プログラ ムの出力結果の概要 |
| 反復測度 SPF-p.q デザインの ANOVA 分析用プ ログラムの例1 |
前節では、SAS による反復測度 SPF-p.q デザインデータを単純な SPF-p.q デ
ザインデータとみなし、glm の test 文を用いて、ANOVA 分析するためのプロ
グラムを示した。
ただし、そこでは同時に、repeated 文を使っての同等な ANOVA 分析プログラムも
示した。しかし、repeated 文を用いると 1.5.5 節でも既に指摘したように、nom
指定を行わないで summary 指定を行うと ANOVA の結果と同時に MANOVA 方式の
主効果や対比検定結果も同時に出力される。2要因以上のデザインでは、さらに
全体的交互作用の MANOVA 方式の検定結果も出力される。
このように、前節では単純な SPF-p.q デザインデータの分析のための SAS
プログラムだけでなく、repeated 文による反復測度 SPF-p.q デザインデータの
ANOVA 分析(MANOVA 方式、正確には GMANOVAを含む分析)プログラムも示し
たが、repeated 文を用いる MANOVA 方式と同等な manova 文によるプログラム
や、族あたりの危険率のコントロールに関する議論は行わなかった。
そこで、この節では、これらについて議論し、そのための SAS プログラム
を示す。
この節で扱うデータは、前節のそれに代えて O'Brien and Kaiser (1985) の
それを用いることにする。O'Brien らのデータも非釣り合い型デザインデータで
あるので、glm の平方和は Type II の方が望ましいと思われるが、彼らは
Type III 平方和を用いており、ここでも彼らの結果と比較するため Type III の
方を用いたプログラムにしてある。
O'Brien らのデータも、実は以下のプログラムで分析してみると、やはり前節
の場合と同様、2ステップ多標本球形仮説は採択される。したがって、repeated
文により出力される ANOVA 分析の部分の F-分布の歪みは無視できることに注意せよ。
プログラムは、以下に示すように repeated 文の出力内容の検討も兼ねたものも
含まれるので、12項から成る。そこで、もし単に repeated 文を用いて反復測
定 SPF_p.q デザインデータの ANOVA 分析を行うには、これらのうち最小限
(1)、(2-1) 及び (2-3) の項のみを実行すれば
よい:
*------------------------------------------------------------------* | December 1, 1998 | | sas program --spf3_3ok.sas | | the final sasprogram for a repeated measures design, especial-| | ly SPF-p.q design data, which appears in O'Brien and Kaiser | | (1985) Table 3, via a complete repeated measures approach. | | It should be noticed that we had better employ weighted null | | hypothesis about group means since the data is unbalanced. As | | a result, we had better choose Type II SS option (ss2) of glm | | procedure. | | | *------------------------------------------------------------------* |
ここでは、冒頭のコメントを記述している。
options ps=60 ls=80; /* (1) data input */ data work; input ssno 2. +1 group 1. +1 (pretest posttest followup) (1.); label ssno='sample number' group='group number to which subject belongs' pretest='mark on a pretest' posttest='mark on a posttest' followup='mark on a follow-up test'; cards; 1 1 233 2 1 434 3 1 657 4 1 534 5 1 464 6 2 899 7 2 589 8 2 356 9 2 445 10 3 478 11 3 356 12 3 698 13 3 668 14 3 256 15 3 377 16 3 578 ; |
この項では、O'Brien and Kaiser (1985) の Table 3 の3群の合計16名の 被験者の事前テスト、事後テスト、及びフォローアップテストの得点から成るデータを 入力するためのプログラムを示す。ここでの独立測定要因は group と名付けた3群 (水準)から成る。また、反復測定要因は3種類のテスト(水準)から成る。
/* (2-1) compute two new variables transformed by orthonormal contrasts */ data work2; set work; z1=(posttest-pretest)/sqrt(2); z2=(followup*2-pretest-posttest)/sqrt(6); run; |
この項では、当該データの反復測定 SPF_3.3 デザインの ANOVA に先立ち、その ために検討すべき多標本球形検定を2ステップで行うとして、当検定の第1ステッ プとしての反復測定変数を正規直交対比により変換した変数間の共分散行列の(群間) 等質性の検定のために、もとの反復測定要因の3水準から構成される変数 pretest、 posttest、及び followup を Helmert 対比を使って変換するためのプログラムを 示す。1.7.4 節の場合と同様、Helmert 対比の係数については、1.7.2 節の 表 1.22を参照されたい。変換後の2変数 は、z1 及び z2 として後続の解析に引き渡される。
/* (2-2) test of homogeneity of covariance matrices on orthonormalized variables */ title 'test of homogeneity of covariance matrices'; title2 '-- necessary for the repeated measures ANOVA--'; proc discrim data=work2 pool=test slpool=0.05; class group; var z1-z2; run; |
/* (2-3) repeated measures SPF-3.3 ANOVA using proc glm repeated statement */ title 'sas glm procedure for a repeated measures design'; proc glm data=work; class group; model pretest posttest followup=group/ nouni; contrast 'control vs exp' group -2 1 1; contrast 'exp1 vs exp2' group 0 -1 1; repeated time 3 contrast(1)/ summary printe printm; output out=temp residual=resid; run; |
この項では、repeated 文による O'Brien-Kaiser データの反復測定 SPF_3.3 デ ザイン ANOVA 分析プログラムを示す。
/* (2-4) repeated measures SPF-3.3 MANOVA (to be precise, GMANOVA) using proc glm manova statement */ title 'test for interaction between group and time'; proc glm data=work; class group; model pretest posttest followup=group/ nouni; contrast 'control vs exp' group -2 1 1; contrast 'exp1 vs exp2' group 0 -1 1; manova h=group m=(-1 1 0, -1 0 1) mnames=pstvspre folvspre/ printh printe summary; run; |
この項では、(2-3) の項での repeated 文による反復測定 SPF_p.q デザイン
データの ANOVA 出力時に付随的に出力される GMANOVA の結果のうち、独立測定
要因と反復測定要因の交互作用の有意性検定と同等な出力を得るための manova 文
によるプログラムを示す。
上のプログラムから明らかなように、repeated 文での変換のオプションである
contrast(1) に対応する manova 文での対比の指定は、m= オプションであり、変換
に contrast(1) を選ぶ場合は、それに対応する対比行列を上のように指定しなけれ
ばならない。また、それらの対比変数の各々に対して、上に示したように mnames=
オプションで変数名をつけなければならない。
title 'test for group main effect'; proc glm data=work; class group; model pretest posttest followup=group/ nouni; contrast 'control vs exp' group -2 1 1; contrast 'exp1 vs exp2' group 0 -1 1; manova h=group m=(1 1 1) mnames=avertime/ printh printe; run; |
この項では、(2-3) の項での repeated 文による反復測定 SPF_p.q デザイン
データの ANOVA 出力時に付随的に出力される GMANOVA の結果のうち、独立測定
要因の有意性検定と同等な出力を得るための manova 文によるプログラムを示す。
交互作用の検定の場合と同様、manova 文での反復測定要因の対比の指定は、m=
オプションであり、独立測定要因の効果のみを検討したい場合には、反復測定要因
の水準は "つぶす" 必要がある。そのためには、それに対応する対比行列を上のよ
うに指定しなければならない。また、その対比変数に対して、上に示したように
mnames= オプションで変数名をつけなければならない。
title 'test for time main effect'; proc glm data=work; class group; model pretest posttest followup=group/ nouni; manova h=intercept m=(-1 1 0, -1 0 1) mnames=pstvspre folvspre/ printh printe summary; run; |
この項では、(2-3) の項での repeated 文による反復測定 SPF_p.q デザイン
データの ANOVA 出力時に付随的に出力される GMANOVA の結果のうち、反復測定
要因の有意性検定と同等な出力を得るための manova 文によるプログラムを示す。
交互作用の検定の場合と同様、manova 文での反復測定要因の対比の指定は、m=
オプションであり、交互作用の検定の時と同じ対比行列を指定することになる。
一方、反復測定要因の効果のみを検討したいので、今度は独立測定要因の水準を
"つぶす" 必要がある。そのためには、manova 文の h= オプションで、上のプロ
グラムのように intercept と指定しなければならない。
/* (2-5) means plot using proc summary */ title 'plot the means for each cell'; proc summary nway print data=work; class group; var pretest posttest followup; output out=workm mean=m1-m3; run; data workplot; set workm; array av(3) m1-m3; do time=1 to 3; aver=av(time); output; end; drop m1-m3; run; options ps=40 ls=80; proc plot data=workplot; plot aver*time=group; run; |
この項は、summary プロシジャ等を用いての反復測定 SPF_3.3 デザインデータ の平均値のプロットを行うプログラムを示す。反復測定 SPF デザインの場合の 例は既に 1.7.4 節でも行ったので、ここでは説明は省略する。
/* (3-1) posterior analysis (1) */ title 'histogram of the error estimates '; proc chart data=temp; vbar resid; run; |
/* (3-2) posterior analysis (2): test for normality of error estimates */ options ps=60 ls=80; title 'test for global normality of the dependent variable'; proc univariate data=temp normal; var resid; run; |
/* (3-3) test for homogeneity of covariance matrices on the original variables for manova-type analysis */ title 'test of homogeneity of covariance matrices'; proc discrim data=work pool=test slpool=0.05; class group; var pretest posttest followup; run; |
この項では、(2-2) の項のプログラムと異なり、もと の反復測定変数間の共分散行列の等質性の検定のためのプログラムを示す。 この検定は、SPF 型のデザイン、すなわち独立測定要因と反復測定要因が混在する デザインでの GMANOVA のための前提条件の1つである。
| spf3-3ok.sas |
うえのプログラムを実行すると、以下のような出力結果が得られる:
Test Chi-Square Value = 4.633776 with 6 DF Prob > Chi-Sq = 0.5916 Since the chi-square value is not significant at the 0.05 level, a pooled covariance matrix will be used in the discriminant function. Reference: Morrison, D.F. (1976) Multivariate Statistical Methods p252. |
この項では、プログラムの (2-2) の項での判別分析プログラムを利用した、反復 測定変数の正規直交対比による変換後の2変数に関するグループ間の共分散行列の 等質性の検定結果を示す。Bartlett の検定結果から、2ステップ多標本球形検定 の第1ステップである正規直交対比による変換後の2変数に関するグループ間の共 分散行列の等質性は、5パーセント水準で採択される。
(2-2) の項の判別分析を実行させ、上のような共分散行列の等質性の検定結果が 出力された後には、一般の判別分析で出力されるその他の各種情報が同時に出力さ れる。しかしながら、ここでは判別分析の目的は単に共分散行列の等質性の検定 のみなので、後続の判別分析に関わる出力は読み飛ばせばよい。
(2-3) の項の repeated 文による反復測定 SPF_3.3 デザインのグループやサン プル数の情報から始まり、repeated 文の contrast(1) で指定した2つの対比変数 間の偏相関行列までの一連の出力結果から成る。これらは読み飛ばせばよい。
Test for Sphericity: Mauchly's Criterion = 0.5446375
Chisquare Approximation = 7.2916171 with 2 df Prob > Chisquare = 0.0261
Applied to Orthogonal Components:
Test for Sphericity: Mauchly's Criterion = 0.8515119
Chisquare Approximation = 1.9289018 with 2 df Prob > Chisquare = 0.3812
|
この項では、(2-3) の項のプログラムによる上記 4. の情報に引き続き出力される
反復測定変数の球形検定結果を示す。このデザインは反復測定 SPF_3.3 デザインな
ので、本来多標本球形検定結果が出力されねばならないが、SAS にはそのオプションは
特別には用意されていないので、(2-2) の項での正規直交対比により変換された変
数でのグループ間共分散行列の等質性の検定に引き続き、ここでは多標本球形検定
の第2ステップの位置づけで 1.7.2 節や 2.1.4 節で述べた球形検定を行っている。
上の結果から、とりわけ直交要素に対して適用された球形検定結果を見ると、p-値
から球形仮説は採択されることがわかる。この結果と上の 2. の結果から、この
データの場合、(2ステップ多標本球形検定の結果)多標本球形仮説は満た
されている、と見れる。
さて、一般的に反復測度 SPF-p.q デザインデータでは、F-比の歪みは、独立測度 要因を G、反復測度要因を S とすると、3つの効果、G、 S、及び G×S のうち S にかかわる部分すなわち S 及び G×S に現れる。一方、SAS を実行すると多標本球形 仮定の成否に拘わらず、自由度修正前の p-値と修正後の p-値を両方並べて出力す るので、この例のように多標本球形仮定が成り立っている場合には、修正しない方 の p-値を見る必要がある。
つぎに、うえの repeated 文で出力される検定結果のうち、ANOVA によるものは、 独立測度要因 Group の主効果とその対比、3種のテストから成る反復測度要 因 Time の主効果、Group と Time の交互作用、Group の対比と Time についての 処理ー対比交互作用 G(-2 1 1)×Time 及び G(0 -1 1)×Time のみ である。
それ以外の repeated 文による出力結果は、MANOVA 方式、正確には GMANOVA に よるもので、それらは Time の主効果、Group と Time の交互作用、Group の対 比と Time についての処理ー対比交互作用 G(-2 1 1)×Time 及 び G(0 -1 1)×Time、ANOVA の出力結果を挟んで、Time の対比 T(-1 1 0)、 Group と Time の対比についての処理ー対比交互作用 G×T(-1 1 0)、その 下位効果としての対比ー対比交互作用 G(-2 1 1)×T(-1 1 0) と G(0 -1 1)×T(-1 1 0)、さらに、Time の対比 T(-1 0 1)、処理ー対比交互 作用 G×T(-1 0 1)、その下位効果としての対比ー対比交互作 用 G(-2 1 1)×T(-1 0 1) と G(0 -1 1)×T(-1 0 1) が、順に出力 される。
ここで注意すべきは、repeated 文で summary オプションを用いると、 このようにして ANOVA と MANOVA 方式の両方の結果が混在して出力 されること、とりわけ対比ー対比交互作用については、ANOVAの結果 と間違いやすい点である。これの点は、うえのプログラムで repeated 文を 用いた (2-3) のやり方と MANOVA 方式に関して同等な後続のプログラム (2-4) の 出力結果を見ると、一部は明らかになる。
Manova Test Criteria and Exact F Statistics for the Hypothesis of no TIME Effect H = Type III SS&CP Matrix for TIME E = Error SS&CP Matrix S=1 M=0 N=5 Statistic Value F Num DF Den DF Pr > F Wilks' Lambda 0.20910927 22.6931 2 12 0.0001 Pillai's Trace 0.79089073 22.6931 2 12 0.0001 Hotelling-Lawley Trace 3.78218866 22.6931 2 12 0.0001 Roy's Greatest Root 3.78218866 22.6931 2 12 0.0001 |
この項では、repeated 文を伴う glm プロシジャにより付随的に出力される GMANOVA の結果の1つである反復測定要因 TIME の主効果の検定結果を示す。この結果から は、GMANOVA によれば TIME の主効果は1パーセント以上の高い水準で有意である。
Manova Test Criteria and F Approximations for the Hypothesis of no TIME*GROUP Effect H = Type III SS&CP Matrix for TIME*GROUP E = Error SS&CP Matrix S=2 M=-0.5 N=5 Statistic Value F Num DF Den DF Pr > F Wilks' Lambda 0.35867769 4.0184 4 24 0.0124 Pillai's Trace 0.64347403 3.0833 4 26 0.0333 Hotelling-Lawley Trace 1.78201942 4.9006 4 22 0.0056 Roy's Greatest Root 1.77864662 11.5612 2 13 0.0013 NOTE: F Statistic for Roy's Greatest Root is an upper bound. NOTE: F Statistic for Wilks' Lambda is exact. |
この項では、repeated 文を伴う glm プロシジャにより付随的に出力される GMANOVA の結果の1つである独立測定要因 GROUP と反復測定要因 TIME の(全体的)交互 作用の検定結果を示す。この結果から、例えば Roy の最大根基準を用いれば、交互 作用効果は、1パーセント水準で有意と言える。また、ヘック chart のパラメータ の1つである s の値が1か2の場合(この場合それに該当)正確な F-統計量とな る Wilks のλ基準では p-値は 0.0124 となっており、この場合、5パーセント水準 で交互作用は有意と言える。
Manova Test Criteria and Exact F Statistics for the Hypothesis of no TIME*control vs exp Effect H = Contrast SS&CP Matrix for TIME*control vs exp E = Error SS&CP Matrix S=1 M=0 N=5 Statistic Value F Num DF Den DF Pr > F Wilks' Lambda 0.40801874 8.7052 2 12 0.0046 Pillai's Trace 0.59198126 8.7052 2 12 0.0046 Hotelling-Lawley Trace 1.45086785 8.7052 2 12 0.0046 Roy's Greatest Root 1.45086785 8.7052 2 12 0.0046 |
この項では、repeated 文を伴う glm プロシジャにより付随的に出力される GMANOVA の結果の1つである独立測定要因 GROUPの対比 G(-2 1 1) と処理(反復測定要因) TIME の処理・対比交互作用の検定結果を示す。
Manova Test Criteria and Exact F Statistics for the Hypothesis of no TIME*exp1 vs exp2 Effect H = Contrast SS&CP Matrix for TIME*exp1 vs exp2 E = Error SS&CP Matrix S=1 M=0 N=5 Statistic Value F Num DF Den DF Pr > F Wilks' Lambda 0.87288817 0.8737 2 12 0.4423 Pillai's Trace 0.12711183 0.8737 2 12 0.4423 Hotelling-Lawley Trace 0.14562212 0.8737 2 12 0.4423 Roy's Greatest Root 0.14562212 0.8737 2 12 0.4423 |
この項では、repeated 文を伴う glm プロシジャにより付随的に出力される GMANOVA の結果の1つである独立測定要因 GROUPの対比 G(0 -1 1) と処理(反復測定要因) TIME の処理・対比交互作用の検定結果を示す。
sas glm procedure for a repeated measures design 53 General Linear Models Procedure Repeated Measures Analysis of Variance Tests of Hypotheses for Between Subjects Effects Source DF Type III SS Mean Square F Value Pr > F GROUP 2 37.35000000 18.67500000 2.91 0.0900 Error 13 83.31666667 6.40897436 Contrast DF Contrast SS Mean Square F Value Pr > F control vs exp 1 37.27814371 37.27814371 5.82 0.0314 exp1 vs exp2 1 0.47727273 0.47727273 0.07 0.7892 |
この項では、repeated 文を伴う glm プロシジャにより出力される独立測定要因 GROUP の主効果の ANOVA 検定結果、及び GROUP の対比検定結果を示す。ここでの 対比検定は、(2-3) のプログラムの項の repeated 文の直前の2つの contrast 文 により指定したもの、すなわち G(-2 1 1) 及び G(0 -1 1) に対してである。 これらの結果は、独立測定要因に関する検定であるので、このデータが反復測定 デザインであるにも拘わらず、F-比の歪みについては最初から全く考慮する必要は ないことに注意されたい。
General Linear Models Procedure Repeated Measures Analysis of Variance Univariate Tests of Hypotheses for Within Subject Effects Source: TIME Adj Pr > F DF Type III SS Mean Square F Value Pr > F G - G H - F 2 27.35783133 13.67891566 19.29 0.0001 0.0001 0.0001 Source: TIME*GROUP Adj Pr > F DF Type III SS Mean Square F Value Pr > F G - G H - F 4 15.40000000 3.85000000 5.43 0.0026 0.0043 0.0026 Source: Error(TIME) DF Type III SS Mean Square 26 18.43333333 0.70897436 Greenhouse-Geisser Epsilon = 0.8707 Huynh-Feldt Epsilon = 1.1486 |
この項では、repeated 文による反復測定 SPF_3.3 デザインの ANOVA 分析結果の
続きとして、反復測定要因 TIME の主効果と、TIME と独立測定要因 GROUP の(全体
的)交互作用についての ANOVA 分析結果を示す。
上述の (2-2) と (2-3) のはじめの方の結果である球形検定の結果から、既に述べた
ようにこのデータでは多標本球形仮説は満たされていると見れるので、ここでの
反復測定要因がらみの2つの効果、すなわち TIME の主効果についても、それと独立
測定要因との(全体的)交互作用についても、F-比の歪みは結果的には考慮する必要
はないことに注意されたい。
Contrast: TIME*control vs exp Adj Pr > F DF Contrast SS Mean Square F Value Pr > F G - G H - F 2 12.32514970 6.16257485 8.69 0.0013 0.0022 0.0013 Contrast: TIME*exp1 vs exp2 Adj Pr > F DF Contrast SS Mean Square F Value Pr > F G - G H - F 2 1.40909091 0.70454545 0.99 0.3838 0.3754 0.3838 |
この項では、repeated 文による反復測定 SPF_3.3 デザインの ANOVA 分析結果の
最後を示す。ここでは直前の全体的交互作用の下位検定の1種である、反復測定要因
TIME を処理とし独立測定要因 GROUP の対比を1つの対比とする、処理・対比交互
作用の検定結果を示している。Contrast につけられたラベルから明らかなように、
前者は T×G(-2 1 1) であり、後者は T×G(0 -1 1) に対するものである。
これらについても、このデータは多標本球形仮説が満たされているので、F-比の
歪みを考慮する必要はないことに注意されたい。
General Linear Models Procedure Repeated Measures Analysis of Variance Analysis of Variance of Contrast Variables TIME.N represents the contrast between the nth level of TIME and the 1st Contrast Variable: TIME.2 Source DF Type III SS Mean Square F Value Pr > F MEAN 1 23.44956971 23.44956971 11.95 0.0043 GROUP 2 20.23571429 10.11785714 5.16 0.0225 Error 13 25.51428571 1.96263736 Contrast DF Contrast SS Mean Square F Value Pr > F control vs exp 1 15.70727117 15.70727117 8.00 0.0142 exp1 vs exp2 1 2.19480519 2.19480519 1.12 0.3095 Contrast Variable: TIME.3 Source DF Type III SS Mean Square F Value Pr > F MEAN 1 52.76153184 52.76153184 47.61 0.0001 GROUP 2 25.59285714 12.79642857 11.55 0.0013 Error 13 14.40714286 1.10824176 Contrast DF Contrast SS Mean Square F Value Pr > F control vs exp 1 20.89824636 20.89824636 18.86 0.0008 exp1 vs exp2 1 2.02922078 2.02922078 1.83 0.1991 |
この項では、repeated 文による
この項は、(2-3) の項の repeated 文による反復測定 SPF_3.3 デザイ ンデータの分析により出力される各種情報のうち、GMANOVA による全体的交互作用 やその部分的交互作用の検定結果と同等の結果を得るための(2-4) のプログラム の項の manova 文を伴う 3種類の glm プロシジャの最初のプログラムの出力結果 の先頭部分で、独立測度要因の水準やグループ数の情報、manova 文の m= の項にユーザが指定した対比行列、対比変数の誤差 SS&CP 行列、そこから計算さ れる偏相関行列、独立測定要因 GROUP に関する 1.6.3 節で述べたH行列、 及び同 1.6.3 節での 行列 HE-1 の特性根(固有根)等 が出力される。ただし、この部分は読み飛ばせばよい。
Manova Test Criteria and F Approximations for
the Hypothesis of no Overall GROUP Effect
on the variables defined by the M Matrix Transformation
H = Type II SS&CP Matrix for GROUP E = Error SS&CP Matrix
S=2 M=-0.5 N=5
Statistic Value F Num DF Den DF Pr > F
Wilks' Lambda 0.35867769 4.0184 4 24 0.0124
Pillai's Trace 0.64347403 3.0833 4 26 0.0333
Hotelling-Lawley Trace 1.78201942 4.9006 4 22 0.0056
Roy's Greatest Root 1.77864662 11.5612 2 13 0.0013
NOTE: F Statistic for Roy's Greatest Root is an upper bound.
NOTE: F Statistic for Wilks' Lambda is exact.
|
この項では、上の 14. の項に続く manova 文による GROUP と TIME の全体的交 互作用の GMANOVA 検定結果を示す。上の結果は、(2-4) のプログラムの3つのう ちの最初のGroup と Time の全体的交互作用に関する結果であり、その後にもしそ れが有意であれば独立測度 Group の3つの水準間の contrast 文で指定する2つ の対比と m= の項で指定する反復測度 Time の3つの水準間の2つの対比を用いた 処理ー対比交互作用と対比ー対比交互作用の検定結果も出力される。もちろん、 ここで出力される部分的交互作用の検定結果は、repeated 文を用いた (2-3) の項の プログラムによるそれらと一致する。
さて、GMANOVA により出力されるうえの結果のうち、まず全体的交互作用につ いては、(2-4) の最初のプログラムにおける独立測度の水準間の対比行列 C が2行3列、反復測度水準間の対比行列が3行2列(SAS の m= の 指定では行と列が逆転していることに注意)であることから、1.6.4 節の (1.209) 式 の Heck チャートのパラメータの値は、(1.184) 式の各行列の行数や列数に注意 すると、

|
(1.228) |

|
(1.229) |
さて、全体的交互作用の (1.184) 式による帰無仮説は、当式による他の帰無 仮説と同様、(1.192) 式の H と (1.193) 式の E を用いて計算され る Roy の最大根や Wilks のラムダ基準の値を用いて、検定できるわけであるが、 そこでも述べたように、一般的にはこれらの値の正確な分布は分かっていない。 そのような場合には、Heck チャート等を用いて検定を行わねばならいことは 既に紹介した通りであるが、やはり 1.6.3 節で簡単に紹介し第3章で詳しく述べる ように、これらの基準の近似統計量を用いた検定も可能であり、SAS ではそれらを 出力する。また、例えば Wilks のラムダ基準については、1.6.3 節でも紹介し たように、 s =1,2 の場合には正確な F-検定量が知られているので、これら を使える。
実際、例えば全体的交互作用に関する帰無仮説は、O'Brien らのデータでは、 うえの議論から s =2 であるので、Wilks のラムダ基準を用いて (1.199) 式に より F-値を計算できる。うえの出力結果から、Wilks のラムダ基準の値 λ \doteq0.35868$ を (1.199) 式に代入すれば、F =4.0184 となり、うえの SAS の Wilks のラムダ基準における F-値に一致することが分かる。また、うえの出力結果 の最後の NOTE の2つ目は、このことを意味している。
もちろん、このような F-検定を行わず Roy の最大根 c1~1.77865 を Heck チャート用に 1.6.3 節で述べた変換式により
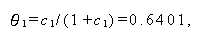
|
(1.230) |
Manova Test Criteria and Exact F Statistics for
the Hypothesis of no Overall control vs exp Effect
on the variables defined by the M Matrix Transformation
H = Contrast SS&CP Matrix for control vs exp E = Error SS&CP Matrix
S=1 M=0 N=5
Statistic Value F Num DF Den DF Pr > F
Wilks' Lambda 0.40801874 8.7052 2 12 0.0046
Pillai's Trace 0.59198126 8.7052 2 12 0.0046
Hotelling-Lawley Trace 1.45086785 8.7052 2 12 0.0046
Roy's Greatest Root 1.45086785 8.7052 2 12 0.0046
|
この項では、(2-4) の項のプログラムにより 15. の項での manova 文による全体 的交互作用の出力結果につづき出力される、TIME を処理とする処理・対比交互作用 の GMANOVA 検定結果を示す。これらは、T×G(-2 1 1) 及び T×G(0 -1 1) である。 それぞれの直前に出力される付随情報については、ここでは省略し、それらの GMANOVA による検定結果のうちの最初の方のみを上に示した。もちろん、これらは (2-3) の項のプログラムにより得られる ANOVA 出力に付随する GMANOVA の結果の 対応部と一致する。
General Linear Models Procedure Multivariate Analysis of Variance Dependent Variable: PSTVSPRE Source DF Type III SS Mean Square F Value Pr > F GROUP 2 20.23571429 10.11785714 5.16 0.0225 Error 13 25.51428571 1.96263736 Contrast DF Contrast SS Mean Square F Value Pr > F control vs exp 1 15.70727117 15.70727117 8.00 0.0142 exp1 vs exp2 1 2.19480519 2.19480519 1.12 0.3095 Dependent Variable: FOLVSPRE Source DF Type III SS Mean Square F Value Pr > F GROUP 2 25.59285714 12.79642857 11.55 0.0013 Error 13 14.40714286 1.10824176 |
この項では、直前の (2-4) の項のプログラムの出力結果に続く、manova 文に
よる GROUP を処理とする処理・対比交互作用、及び GROUP の1つの対比と TIME
の1つの対比に関する対比・対比交互作用の GMANOVA 検定結果を示す。
ここでの TIME の対比には、(2-4) の項のプログラムの中の mnames= の項で
PSTVSPRE、FOLVSPRE なる名前を付けていることを思い出してほしい。上の結果は、
これら2つの反復測定要因 TIME の対比ごとに、Source の項で処理・対比交互作用
を、Contrast の項で独立測定要因 GROUP と反復測定要因 TIME のそれぞれの対比
に対応する対比・対比交互作用の検定結果を示す。
例えば、最初の TIME 対比 PSTVSPRE は、T(-1 1 0) であるが、まず GROUP の
項では G×T(-1 1 0) の検定結果が、つぎの Contrast の項では順に
G(-2 1 1)×T(-1 1 0)、G(0 -1 1)×T(-1 1 0) なる対比・対比交互作用検定結果が
示されている。もちろん、これらの検定結果は、(2-3) の項の repeated 文を用いた
ANOVA 結果に付随する GMANOVA 出力結果に一致している。
出力のまとめとして、これらの 15. から 17. までの出力結果からわかるように、
(2-4) のプログラムの項の最初の manova 文による反復測定 SPF_3.3 デザインデータ
の GMANOVA による出力では、反復測定要因 TIME の主効果、及びその対比検定は
行われない点に注意したい。
いずれにせよ、これらの計算方式から明らかなように、SAS の場合、反復測定 デザインにおける repeated 文における contrast 項で出力される対比検定(これを manova 文で行うのが、上の結果)では族あたりの危険率のコントロールがなされ ない。このデザインの場合の族をどう見るかにより、危険率のコントロールの仕方 は変わるが、例えば全体的交互作用の下位検定を対比ー対比交互作用とみなす とすれば、どうすれば族あたりの危険率のコントロールができるであろうか。
そのためには、2通りの方法がある。1つは、SAS/IML を用いる方 法である。というのは、SAS/STAT の通常の repeated 文や manova 文を用いるやり 方では、(1.184) 式の帰無仮説 に対して (1.207) 式の Roy-Bose 方式による同時検定を実行させることはできないが、SAS/IML を用いれば (1.207) 式の左辺の値を計算できるので、Heck チャートからその場合のパラメー タ値に対応する xα を読みとり、両者を比較すればよいからである。
もし SAS/IML が利用できない場合には、どうすればよいであろうか。 このような場合には、GMANOVA 方式により出力された F-値を用いてうえの検定を 行うことができる (O'Brien & Keiser, 1985)。彼らは、この方式を Scheff\'e 方 式の検定と言っているが、Roy-Bose 方式に他ならない。ただし、この方法は (1.207) 式の左辺の値と Heck チャートを利用するのではなく、GMANOVA による 各対比ー対比交互作用等の(族あたりの危険率をコントロールしていない)F-値 と Heck チャートとを用いる方法である。
具体的には、F を GMANOVA 方式により出力された、したがって repeated 文 もしくは manova 文により出力された F-値、FS を彼らの言う Scheff\'e 方式の F-値とすると、(1.207) 式をつぎのように見るのと同等である:
つまり、全体的交互作用に関する帰無仮説が棄却されたとき、すべての下位 対比ー対比交互作用の検定の族あたりの危険率を 100α パーセントに押さ えた同時検定の棄却点を、
|
とすればよい。
O'Brien らのデータの場合、Roy の最大根を用いて (1.230) 式で既に計算し Heck チャートで読み取った xα の値 0.498、サンプル数 N =16、及び 独立測度の水準数 I =3 を上式に代入すると、FS =12.9 となる。
これに対して、repeated 文等で出力される GMANOVA 方式による F-値は、 G(-2 1 1)×T(-1 1 0)、G(0 -1 1)×T(-1 1 0)、 G(-2 1 1)×T(-1 0 1)、及び G(0 -1 1)×T(-1 0 1) の順に、8.00、 1.12、18.86、及び 1.83 である。したがって、これらの結果から 12.9 を越えて いる G(-2 1 1)×T(-1 0 1) のみが、族あたりの危険率を5パーセントに コントロールした場合、統計的に有意であるといえる。
もし、これを行わないで、SAS の repeated 文もしくは manova 文によるこれら 個々の対比ー対比交互作用の出力結果によれば、p-値は順に、0.0142、0.3095、 0.0008、及び 0.1991 となり、G(0 -1 1)×T(-1 1 0) と G(-2 1 1)×T(-1 0 1) の2つが有意となることに注意せよ。
いずれにせよ、Scheff\'e 方式の危険率のコントロールは、 O'Brien らも指摘しているように、一般に検出力が劣るとしばしば批 される。。しかし、彼らも指摘しているように、このような批判もつぎのよう にすれば回避できる。すなわち、うえのデータの場合、族を全体的交互作用(のす べての下位検定)とせず、例えば G(-2 1 1)×T、すなわち処 理ー対比交互作用の1つを族とみなせばよい。
このようにみなすと、このデータの場合 GMANOVA の帰無仮説 (1.184) 式 において
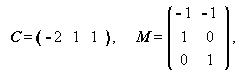
|
(1.232) |

|
(1.233) |

|
(1.234) |
この場合、s =1 なので (1.231) 式の FS は、
|
となる。ここで、
|
したがって、この場合 (1.235) 式における FS の右辺の F の2つの自由度 は、(1.236) 式から ν1=2 及び ν2=12 となる。そこで、通常の F-分布 表もしくは SAS/STAT の probf 関数による計算から、これらの自由度の場合の5 パーセント棄却点の値は、3.89 となる。これらより、(1.235) 式の FS =8.42 と 計算できる。
もちろん、この場合には G(-2 1 1)×T の下位検定 は、G(-2 1 1)×T(-1 1 0) 及び G(-2 1 1)×T(-1 0 1) の2つである。 いずれにせよ、この場合の棄却点の値 8.42 は、族を全体的交互作用と見た時 の 12.9 と比べて小さくなっていることが分かる。すなわち、検出力は相対的に は上がったことになる。
この項では、(2-4) のプログラムの3種の manova 文によるプログラムの2つ目の それによる独立測定要因 GROUP 主効果及びその対比の GMANOVA 検定結果を示す。 それらは、すべて (2-3) のプログラムの GROUP の主効果及びその対比の ANOVA 検定結果に等しい。なぜならば、この場合、反復測定要因の対比を manova 文の m= の項で m=(1 1 1) としている、すなわち反復測定要因の3水準の値をいわば つぶしているので、結果的には独立測定要因が1つの ANOVA に帰着されるからで ある。
この項では、(2-4) のプログラムの3種の manova 文によるプログラムの3つ目の それによる反復測定要因 TIME 主効果及びその対比の GMANOVA 検定結果を示す。 それらは、すべて (2-3) のプログラムの TIME の主効果及びその対比の GMANOVA 検定結果に等しい。なぜならば、この場合、独立測定要因の効果を manova 文の h= の項で h=intercept としている、すなわち独立測定要因の3水準の値をいわば つぶしているので、結果的には反復測定要因が1つの GMANOVA に帰着されるからで ある。
plot the means for each cell 72
GROUP N Obs Variable Label N Mean
-------------------------------------------------------------------------
1 5 PRETEST mark on a pretest 5 4.2000000
POSTTEST mark on a posttest 5 4.0000000
FOLLOWUP mark on a follow-up test 5 4.4000000
2 4 PRETEST mark on a pretest 4 5.0000000
POSTTEST mark on a posttest 4 6.5000000
FOLLOWUP mark on a follow-up test 4 7.2500000
3 7 PRETEST mark on a pretest 7 4.1428571
POSTTEST mark on a posttest 7 6.5714286
FOLLOWUP mark on a follow-up test 7 7.2857143
-------------------------------------------------------------------------
|
この項では、(2-5) のプログラムの中の summary プロシジャによる反復測定 SPF_3.3 デザインの合計9のセルの各々の平均値、標準偏差、最大値、及び最小値 を出力する。ここでは、平均値のみを示した。
plot the means for each cell 74
プロット : AVER*TIME. 使用するプロット文字 : GROUP の値.
8 +
|
|
|
|
| 2
|
7 +
|
|
AVER | 2
|
|
|
6 +
|
|
|
|
|
|
5 +2
|
|
|
| 1
|
|1
4 + 1
-+-----------------------------------+-----------------------------------+-
1 2 3
TIME
|
この項では、直前の 20. の項で計算した各セルの平均値を (2-5) の項のプログラム の中の plot プロシジャにより描かせた結果を示す。図中、横軸は反復測定要因 の3水準を、第1象限の数字は独立測定要因の水準をそれぞれ示す。
histogram of the error estimates 75
Frequency
6 + *****
| *****
| *****
| *****
| *****
5 + *****
| *****
| *****
| *****
| *****
4 + *****
| *****
| *****
| *****
| *****
3 + ***** ***** ***** *****
| ***** ***** ***** *****
| ***** ***** ***** *****
| ***** ***** ***** *****
| ***** ***** ***** *****
2 + ***** ***** ***** *****
| ***** ***** ***** *****
| ***** ***** ***** *****
| ***** ***** ***** *****
| ***** ***** ***** *****
1 + ***** ***** ***** ***** *****
| ***** ***** ***** ***** *****
| ***** ***** ***** ***** *****
| ***** ***** ***** ***** *****
| ***** ***** ***** ***** *****
--------------------------------------------------------------------
-1.8 -0.6 0.6 1.8 3.0
RESID 中間点
|
この項では、(3-1) の項のプログラム chart プロシジャにより、モデルの誤差項の ヒストグラムを描いたものである。
test for global normality of the dependent variable 76
Univariate Procedure
Variable=RESID
Moments
N 16 Sum Wgts 16
Mean 0 Sum 0
Std Dev 1.584448 Variance 2.510476
Skewness 0.273758 Kurtosis -0.84484
USS 37.65714 CSS 37.65714
CV . Std Mean 0.396112
T:Mean=0 0 Pr>|T| 1.0000
Num ^= 0 16 Num > 0 7
M(Sign) -1 Pr>=|M| 0.8036
Sgn Rank -7 Pr>=|S| 0.7338
W:Normal 0.948232 Pr <W 0.4518
Quantiles(Def=5)
100% Max 3 99% 3
75% Q3 1.328571 95% 3
....................
....................
....................
|
この項では、(3-2) のプログラムの univariate プロシジャでモデルの誤差項の 正規性の検定結果を示す。
Test Chi-Square Value = 11.134799
with 12 DF Prob > Chi-Sq = 0.5174
Since the chi-square value is not significant at the 0.05 level,
a pooled covariance matrix will be used in the discriminant function.
|
この項では、(3-3) の discrim プロシジャにより、(2-4) の manova 文 を伴う glm プロシジャによる GMANOVA や、(2-3) の repeated 文による反復測定 ANOVA 出力結果に付随的に表示される GMANOVA の 適用の前提である、もとの反復測定変数間の共分散行列の等質性の検定結果を示す。 この検定は、(2-2) 節での反復測定変数を正規直交対比により変換後の変数数の 1つ少ない場合の共分散行列の等質性の検定とは異なることに注意されたい。