2-9-1 節 多重共線性とその対処法
このページは、平成２８年８月２６日に開設しました。
このページは、令和２年５月７日に一部更新しました。
多重共線性 (multicollinearity) 或いは 共線性 (collinearity) なる概念に対する正確な定義 は、Belsley, Kuh, and Welsch (1980) によれば、文献上では完全には確立していない。彼らによ れば、文字通りに言えば、２変数のデータベクトルが同一線上に位置するならば、２変数は共線 性がある、という。多変数に拡張すれば、k 変数のデータベクトルが k より低い 次元の部分空間内に位置するならば、k 変数は共線性がある、という。ただし、実際の データでは、この状態そのものが起こることはまれであり、これに近い状態が起こっている可能性 があるという。
それでは、多重共線性あるいはそれに近い状態が起こっている場合、何が問題になるのであろ うか。実は多重共線性が生起していると、2.2 節で述べた重回帰分析 での各説明変数に対する重み係数、正確には偏回帰係数に影響が現れ、その正確な推定ができなく なるのである。ここで、2.2 節の (2.12) 式 を見てみよう。(2.12) 式を再度示すと、つぎのようである：
|
(2.12) |
(2.12) 式は、偏回帰係数の推定値を求める公式であるが、 その式の右辺は、全サンプルの説明変数の観測値（各変数とも全サンプルの平均を引いたものが 入るが）から成る行列 Xm 及び基準変数の観測 値ベクトル yB（こちらも全サンプルの基準変 数の平均値を引いたもの）から成ることがわかる。なお、ここで (2.12) 式の左辺は、m 個 の説明変数の偏回帰係数の推定値で、定数項 β0 を含まないことに注意したい。
上記の議論からは、重回帰分析における多重共線性の議論は基準変数と は何ら関係がない という点である。多重共線性の問題は、もっぱら重回帰分析における 説明変数間の関連にのみかかわることに注意する必要がある。したがって、この問題は基準変数 が定性的変数の場合の重回帰分析的方法である ロジスティック回帰分析 の場合にも成り立つ議論なのである。
Belsley, Kuh, and Welsch (1980) によれば、多重共線性の有無は全サンプル（N 人）の 全説明変数（m 変数）の観測値から成る N×m 行列 Xm の 特異値 (singular value）が m 個あるとし、それらを μ1, μ2, …,μm と書けば、それらのうちの最大のものを μmax とすれば、データ行列 Xm の次式で定義される m 個の 条件指標 (condition index) の値を検討することにより 推論できるという：
|
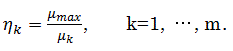
(2.76) |
ここで、任意の N×m 行列 Xm の特異値は、一般にXm Xtm あるいは Xtm Xm の 固有値 (eigenvalue) の平方根とし て求めることができる。
条件指標は説明変数の数だけ計算されるが、条件指標の値が最大となるのは行列 Xm の特異値のうち (2.76) 式の分子の最大値 µmax に対して同分母のそれが最小値となる場合である。さらに、データ行列 Xm の特異値のうちの最小なものが小さな値であると、対応する行列 XtmXm の最小固有値も小さくなる。その ような場合、2.2 節の (2.12) 式で示されている重回帰分析における偏回帰係数の推定式の 右辺の逆行列の計算は、スカラーの逆数の計算の場合ゼロに近い値で割り算をすることに近 い状況が生起するため、偏回帰係数の推定が不安定になることになる。それに対して、(2.12) 式の右辺のyB はベクトルであり、偏回帰係数の推定に際して逆行列の 操作がないため、そのような影響はでないことがわかる。
Belsley, Kuh, and Welsch (1980) によれば、条件指標の値が ５から１０あたりまでならば弱い従属性 (weak dependency)（言 い換えれば、 弱い共線性）が、同じく３０か ら１００あたりであれば強い関係（言い換えれば、強い共線性 ）があるといえる。
統計ソフト、例えば SAS の重回帰分析で多重共線性を指定すると、偏回帰係数の推定と検定 の出力のつぎに共線性の診断結果が出力される。そこには、上記固有値の大きい順に、固有値及 び条件指標の値等が出力されているので、最後の説明変数（固有値の最小の変数）の条件指標 を見て、その値がうえの値の範囲のどこに入っているかを見て、共線性の有無を診断することが できる。なお、SAS の重回帰分析の多重共線性がらみのパラメータのうち、collinoint パラメータ を指定すると、(2.76) 式のｍ個の条件指標が出力されるが、collin パラメータを指定すると ｍ＋１個の条件指標が出力される。これは、偏回帰係数の推定に定数項β0 を含 める場合の条件指標に対応する。これについては、後述する。どちらを使うべきかは、 データの性質等に依存する。
なお、説明変数に定性的な変数が混在する場合は、あらかじめそのような変数については ダミー変数化した新たな変数をプログラムで定義したうえで、多重共線性を指定して重回帰 分析を行えばよい。
つぎに、それではどの変数（複数）が多重共線性の原因になっているかを見つければよいで あろうか。これを行うための１つの方法は、分散インフレ因子 (variance inflation factors)（あるいは分散拡大因子） （VIF と略記される）を計算することである。この指標は、 上記条件指標と同様に、説明変数ごとに計算され、次式で定義される：
|
(2.77) |
ここで、この式の右辺の R2k は、k 番目の説明変数をそれを 除く説明変数で説明した時の重相関係数を指す。
(2.77) 式から明らかなように、分散インフレ因子の値が大きくなる説明変数は、その変数を それ以外の説明変数で説明した時の説明力が大きな変数であり、その変数は他の説明変数の線形 和で近似できることを示しているため、そのような説明変数は多重共線性に関与している可能性 があると見れる。例えば、統計ソフト SAS では、多重共線性の出力を指示すると、重回帰分析 の「パラメータの推定値」の項に、偏回帰係数の推定値、標準誤差、t 値、p-値などに引き続い て、「分散拡大」の項が出力されるので、最大条件指標の値が相対的に大きい場合、この項をみて、 分散拡大の値の大きい変数を除去するのが、当該データの多重共線性に対応する１つの方法 である。
最後に、重回帰分析を用いて偏回帰係数の推定に定数項β0 を含める場合、なぜ 条件指標が説明変数の数 m ではなく m+1 必要なのかを以下に述べる。そのためには、最初に 無修正平方和行列 (uncorrected sums of squares and cross product matrix) 及び無修正相関行列 (uncorrected correlation matrix) なる概念が必要となる（例えば、Carey, 1998; Iacobucci et al., 2015)。これら を説明するために、まず次の２つの行列を定義する。
|
(2.78) |
|
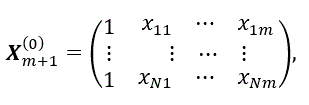
(2.79) |
ここで、前者は N 行 m 列の説明変数の値を要素とする行列で、各説明変数の値から平均を引 かない素データ行列である。一方、後者は、N 行 m+1 列の行列で、第１列の要素はすべて１で 第２列から第 m+1 列までは、前者の行列そのものである。
つぎに、(2.79) 式の行列を用いて
|
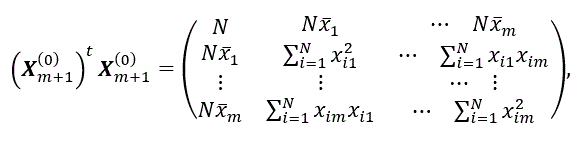
(2.80) |
を定義しよう。(2.80) 式の右辺の行列は無修正平方和行列と呼ばれる。
つぎに、(2.80) 式の行列の対角要素の平方根を要素とする m+1 行 m+1 列の対角行列を つぎのように定義するものとする：
|
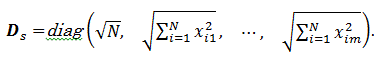
(2.81) |
(2.79) 式と (2.81) 式を用いると、つぎに示す m+1 行 m+1 列の 無修正相関行列を定義できる：
|
(2.82) |
ここで、(2.82) 式で定義される無修正相関行列の要素は、通常の相関行列とは若干異なる が、各要素は如何なる範囲の値を取るのであろうか。もちろん、通常の相関行列を構成する それぞれの要素は相関係数であるので、－１から１の範囲になるが、無修正相関行列 の要素は同じ範囲をとるであろうか。答えは通常の相関係数の場合と同じで、すべて－１ から１の範囲になる。このことは、シュワルツの不等式 、とりわけ２つのベクトルに 関するシュワルツの不等式を考えれば、簡単に証明できる。すなわち、(2.82) 式の行列の 第２行第２列以降の非対角要素は、対応する２つの説明変数についての N 人のサンプルの値 を要素とするベクトルについてのシュワルツの不等式を、第１行及び第１列の非対角要素 については、いずれかの説明変数の N 人のサンプルの値を要素とするベクトルと要素が すべて１の N 次ベクトルについてのシュワルツの不等式を定義すれば自明である。
つぎに、
|
(2.83) |
及び
|
(2.84) |
を定義すると、重回帰方程式より、
|
(2.85) |
が得られる。これより、(2.80) 式及び (2.82) 式に注意すれば定数項を含む m+1 次の 偏回帰係数の推定値ベクトルは
|
(2.86) |
と書ける。
ここで、(2.86) 式と上で再定義した (2.12) 式とを比較してみよう。(2.12) 式の右辺
の行列 
に対応する
(2.86) 式の右辺の行列はTであることに注意すれば、Tの固有値の中に小さい
ものが存在する場合、βm+1 の推定は不安定になることがわかる。
次節、すなわち 2.9.2 節の多重共線性への対処法・適用例の項で述べるように、SAS の
REG プロシジャ (proc reg) では、多重共線性のオプションに collin 及び collinoint
オプションの２種類が用意されている。これらは順に、うえの２つの行列 T 及び
に対応する。
より正確には、前者は定数項を含めた m+1 行 m+1 列の無修正相関行列の固有値に
対応する条件指標を出力させるのに対して、後者は行列
をもとにした m 個の説明変数間の通常の相関行列の固有値に対応する条件指標を出力させ
る。このことを SAS プログラムで確認するためには、SAS の PRINCOMP プロシジャ (proc
princomp) を次のように用いるとよい。
1) SAS の PRINCOMP プロシジャによる無修正相関行列及び通常の相関行列の固有値計算
*----------------------------------------------------------------------*
| September 24, 2016 |
| sas program--logistic-analysis1-revised-for-Takai.sas-- |
| a sasprogram for a fundamental analysis of Takai's thesis data.|
| |
*----------------------------------------------------------------------*;
libname sasfile 'c:\permfile';
options pagesize=60;
data work;
set sasfile.takai;
corres=(nocor/18-tnsm/12);
sorerr=(tserr/18-tdifm/12);
falrat=(tfrec/6-tnfr/4);
remc=norem/nocor;
if tfrec ne 0 then remf=nofrem/tfrec;
else remf=0;
if tserr ne 0 then rems=nosrem/tserr;
else rems=0;
if tnsm ne 0 then remnonc=nsmrem/tnsm;
else remnonc=0;
if tdifm ne 0 then remnons=difmrem/tdifm;
else remnons=0;
if tnfr ne 0 then remnonf=nfrrem/tnfr;
else remnonf=0;
crate=remc-remnonc; srate=rems-remnons; frate=remf-remnonf;
nopre=tnsm+tdifm+tnfr;
const1=1;
output;
run;
/* Analysis for */
/* the crest variable */
data temp1;
set work;
if corres ge 0.63 then crest=1;
else crest=2;
lavtav=lav*tav;
stantran=stanx*tranx;
output;
run;
title 'PC for the correlation matrix between 5 vars.';
proc princomp data=temp1;
var lav tav lavtav stanx tranx;
run;
title 'PC for the correlation matrix between 6 vars. (2)';
proc princomp data=temp1 noint;
var const1 lav tav lavtav stanx tranx;
run;
|
うえのプログラム中の data 文の下方の 「const1=1; 」により、各サンプルごと、新たに 値が１なる変数 const1 が生成される。最後の２つの PRINCOMP プロシジャのうちの最初の 方は、lav から tranx までの５変数のデータから通常の相関行列 を計算し、その固有値を計算する。これにより得られる５変数データの固有値は、2.9.2 節 で述べる同一データに対して適用した場合の多重共線性検討のための重回帰分析プロシジャ における collinoint パラメータを指定したときに得られる条件指標計算時に出力される固 有値と一致する。
一方、最後のPRINCOMP プロシジャでは、前者の PRINCOMP プロシジャでの５変数に data 文により生成された値１から成る変数 const1 を加え、さらに同プロシジャに noint オプ ションを追加しており、これにより上述の (2.82) 式で定義した 無修正相関行列の固有値が計算される。そして、この固有値は 同じく2.9.2 節で述べる同一データに対して適用した場合の多重共線性検討のための重回帰 分析プロシジャにおける collin パラメータを指定したときに得られる条件指標計算時に出 力される固有値と一致する。
2) SAS の PRINCOMP プロシジャによる通常の相関行列及び無修正相関行列及びの固有値
PC for the correlation matrix between 5 vars. 1
2016年10月17日 月曜日 12時56分33秒
PRINCOMP プロシジャ
オブザベーション数 30
変数の数 5
単純統計量
lav tav lavtav stanx tranx
Mean 0.5000000000 0.5000000000 0.2333333333 44.43333333 52.23333333
StD 0.5085476277 0.5085476277 0.4301830672 9.22023013 11.06308971
相関行列
lav tav lavtav stanx tranx
lav 1.0000 -.0667 0.5517 -.1434 0.0153
tav -.0667 1.0000 0.5517 0.0478 -.1747
lavtav 0.5517 0.5517 1.0000 -.1046 -.1133
stanx -.1434 0.0478 -.1046 1.0000 0.7390
tranx 0.0153 -.1747 -.1133 0.7390 1.0000
相関行列の固有値
固有値 差 比率 累積
1 1.94302960 0.39887381 0.3886 0.3886
2 1.54415580 0.43471562 0.3088 0.6974
3 1.10944017 0.88340013 0.2219 0.9193
4 0.22604004 0.04870564 0.0452 0.9645
5 0.17733439 0.0355 1.0000
固有ベクトル
Prin1 Prin2 Prin3 Prin4 Prin5
lav 0.345426 0.340911 0.692764 0.344893 0.406924
tav 0.348258 0.350990 -.687024 0.060019 0.529072
lavtav 0.520102 0.499219 0.010572 -.296847 -.626135
stanx -.486276 0.516558 -.151758 0.623949 -.290448
tranx -.502421 0.494504 0.157901 -.632468 0.279447
PC for the correlation matrix between 6 vars. (2) 5
2016年10月17日 月曜日 12時56分33秒
PRINCOMP プロシジャ
オブザベーション数 30
変数の数 6
単純統計量
const1 lav tav lavtav stanx tranx
Mean 1.000000000 0.5000000000 0.5000000000 0.2333333333 44.43333333 52.23333333
UStD 1.000000000 0.7071067812 0.7071067812 0.4830458915 45.34864937 53.35385022
無修正相関行列
const1 lav tav lavtav stanx tranx
const1 1.0000 0.7071 0.7071 0.4830 0.9798 0.9790
lav 0.7071 1.0000 0.4667 0.6831 0.6726 0.6945
tav 0.7071 0.4667 1.0000 0.6831 0.6996 0.6671
lavtav 0.4830 0.6831 0.6831 1.0000 0.4550 0.4527
stanx 0.9798 0.6726 0.6996 0.4550 1.0000 0.9894
tranx 0.9790 0.6945 0.6671 0.4527 0.9894 1.0000
無修正相関行列の固有値
固有値 差 比率 累積
1 4.48511887 3.64164833 0.7475 0.7475
2 0.84347054 0.30872473 0.1406 0.8881
3 0.53474581 0.42896063 0.0891 0.9772
4 0.10578518 0.08402799 0.0176 0.9949
5 0.02175719 0.01263477 0.0036 0.9985
6 0.00912242 0.0015 1.0000
固有ベクトル
Prin1 Prin2 Prin3 Prin4 Prin5 Prin6
const1 0.450950 -.291937 -.000332 -.081586 -.839497 -.002282
lav 0.381796 0.239787 0.706088 0.541383 0.068858 -.018349
tav 0.381763 0.240610 -.706223 0.538338 0.069210 0.054912
lavtav 0.328261 0.756728 0.000858 -.564232 -.031947 -.015102
stanx 0.446323 -.334252 -.036728 -.190890 0.376493 -.713818
tranx 0.445166 -.339147 0.036590 -.235889 0.378081 0.697767
|