(5.10) 式の t ' の自由度を
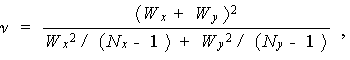
|
(5.12) |
として、t-検定を行う。
この授業では、母集団の分散が等質でない場合、(b) の
Satterthwaite (1946) の方法を用いよ。なお、この方法は内外の多くの
テキストでは Welch 法(Welch, 1947) と呼ばれているものであるが、SAS では
Satterthwaite の方法と呼ばれており、ここでもこれを踏襲した。
5.2.3 母分散の等質性が採択される場合の平均の差の検定における
危険率の計算方法
2組の標本に対して両母分散が等しいかどうか不明で母分散の等質性の検定を行って等質性仮説が採択され
たとしよう。従来、内外の統計学のテキストの多くは、母分散の等質性が採択されようが棄却されようが、
一律にそれぞれの検定を例えば5%有意水準を設定して検定する方式しか既述していないが、Hogg (1961)
によれば、例えば、それぞれの検定の危険率をα=0.01 に取るとした場合、全体の検
定での危険率は実際には α*= 0.0199... ~ 0.02となり、
危険率のインフレをまねくことになる。
この問題を回避するためには、分散の等質性が採択される場合には、Hogg (1961) が指摘しているように、
等質性の検定も平均の差の検定も、例えば全体の危険率をα*= 0.05 にしたければ、個々の危険率を
およそ 0.025 に、もしα*=0.01 にしたければ、個々の危険率をおよそ 0.005 に取ればよい。
ちなみに、授業の演習で、例えば2組の標本の標本数が共に20の場合には、F検定と分散
が等しい時の t 検定における、全体の危険率α* が5パーセントの場合と1パーセントの場合に対応
する棄却点の値は、つぎのようになる:
- 分散の等質性の F検定の危険率と棄却点の値
- 分散が等しいときの t検定の危険率と棄却点の値
これらの値は(通常のF分布表には掲載されていないが)、本テキストの末尾の表で見ることが
できる。例えば、分散の等質性のF検定の棄却点の値は、通常のF分布表がF分布の右端のみに対応する
ものであるので、α*に対応するF値であれば、0.025/2、すなわち、p=0.0125 で2つの自
由度が19 の場合を見ることになり、付表 7-2を見る必要がある。一方、分散が等しい時のt検定の
棄却点の値は、通常両側検定に対応するものであるので、同じくα* に対応するt値であ
れば、付表4で p=0.025 で自由度38の場合を見ればよい。
一方、諸君が WEB 上で演習結果をチェックするために情報処理教育センターの統計ソフト SAS を
用いて検定を行う場合には、F値や t値に対する p-値を直接計算して出力してくれるので、検定時には、
うえのような棄却点の値を見る必要はなく、例えば全体の検定での危険率を5
%とするならば、F検定での p-値が 0.0125 以下かどうか、またt検定でのp-値が0.025以下か
どうかのみチェックすればよい。
5.2.4 母分散の等質性が棄却される場合の平均の差の検定における危険率の計算方法
平均の差の検定に先立つ分散の等質性検定で分散の等質性仮説が棄却された場合には、それぞれの帰無仮説の
もとでの2つの統計量は互いに独立にはならず、そのような場合、例えば Hogg (1961)は、たとえ平均の
差が統計的に有意であっても、決定的な結論は下さず後続の研究にゆだねる必要がある、といっている。
また、竹内 (1973, p.19) は、もし分散の等質性が棄却されるという条件下で両群の平均の差の
検定をすることは無意味であろう、と言っている。ただし、この点について言及しているテキストもきわめ
て少ない。
ただし、この授業ではうえのような議論のあることは頭に入れたうえで、従来の多くのテキスト
と同様に、Satterthwaite (1946) の方法(Welch, 1947) を用いて平均の差の検定を行うこととする。
この場合、うえに記したように、分散の等質性のF検定と平均の差のt検定は独立にはならないので、
正確な全体的有意水準の計算ができないが、ここでは平均の差のt検定の危険率(有意水準)は、5.2.3
節の場合に準じて行うものとする。つまり、例えば全体の危険率が5%ならば、t検定での危険率は
0.025 とするものとする。ただし、分散が等しい場合の(5.9) 式ではなく、(5.10) 式を用い、なおかつ
自由度の計算にはSatterthwaite (1946) の方法を用いるので、この場合の自由度の計算は(5.12) 式を
用いること。
互いに独立な2組の標本 x 1 , x 2
, ... , x Nx (標本数 N x )
及び y 1 , y 2 , ... ,
yNy (標本数 N y )を手
にしたとき、母集団の平均に差があるかどうかの有意性検定(平均の差の
検定)を行う方法を学ぶ。
2組の標本が得られた母集団の分布形が未知か既知か、母分散は既知かどうか、
さらには母集団の分散が等質かどうかの違いにより、検定方式を変える必要がある。
卓上計算機を用いて、互いに独立な2組の標本 x 1 , x 2 , ... ,
x Nx(標本数 N x )及び y 1 ,
y 2 , ... , y Ny(標本数 N y )が
得られたもとの母集団の平均に差があるかどうかの有意性検定を行え。

5.6.1 5.1 節の、母集団の分布形が未知の場合
ここでは、5.1 節のケース、すなわち母集団の分布形は2組とも未知で、母分散
σ x2 、及び σ y2
が既知で、それぞれ σ x02 、及び
σ y02
標本数が大の場合に、 N 個の無作為標本を手にしたとき標本が得られたもと
の母集団の平均の区間推定を行う計算の手順について述べる。
母集団の分散の情報については、当日配布する各人の問題用紙の中に記
されている母標準偏差 σ x0 及び σ
y0(母分散ではない!)の
値を読みとること。計算の手順はつぎの通りである:
- 2組の標本の平均
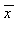 、及び
、及び
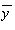 を求める。
を求める。
- 5.1.2 節の | z | の計算をする。(ここで、計算に際して、棄却点
z
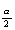 の値は、問題用紙で指定
された危険率に対応するものを選ばねばならないことに注意せよ)。
の値は、問題用紙で指定
された危険率に対応するものを選ばねばならないことに注意せよ)。
5.6.2 5.2 節の、母集団の分布が正規分布の場合
ここでは、5.2 節のケース、すなわち母集団の分布形は2組とも正規分布である
ことが分かっているが、母分散 σ x2 、及び
σ y2 は共に未知である時、
N x 個及び N y 個の互いに独立な無作為標
本を手にしたとき、標本が得られたもとの母集団の平均の区間推定を行う計算の手順
について述べる。計算の手順はつぎの通りである:
- 2組の標本の平均
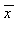 、
及び
、
及び 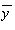 を求める。
を求める。
- 2組の標本の分散 s x2 、及び s
y2 を求める。
- (5.6) 式の F 値を計算する。
- うえの F 値を、付表 7-1 または 7-2 のうちの適切な自由度に対応する
危険率に応じた棄却点の値と比較し、そこに記した方法で、分散の等質性の検定を行う。
ただし、宿題で統計ソフト SAS を用いる場合には、棄却点の値ではなく直接 SAS
SAS の出力中の p-値で判断すればよい。
- 平均の差の検定
実習レポート記入の仕方は、以下に示すように、5.2 節の、母集団の分布形が正規分
布の場合のみであるので注意せよ。
以下の項目について、すべて小数第3位を四捨五入して、小数第2位までの数値を出
席カードの裏側に順に書き写せ。その際、以下に従い、一行一項目または2項目とし、
例えば 1. x の平均 32.50、y の平均 46.70 のように書くこと。
- x の平均、y の平均
- F 値 ( F )
- F の第1自由度 (ν 1 )、 F の第2自由度 (ν 2
)
- F 検定結果(棄却、又は採択)
- X の標準偏差 ( s x )、 Y の標準偏差
( s y )
- t(又は t')の値、 t(又は t')の自由度( ν )
- t 検定結果(棄却、又は採択)


これまで、手計算による平均の差の検定の計算方法について述べてきたが、
サンプル数が大きくなると、たいへんな手間がかかる。このような作業は
本来人間には向かない。原理さえわかれば、諸君は今やこの種の検定を手計算
でやる時代ではない。以下の2つの例は、国際的な統計ソフト SAS を用いた平均
値の差の検定、とりわけ t-検定等の手順を示す。
ここでは、2群の平均の差の検定、とりわけ t-検定や、正規性の検定、その
他の分析を行うための SAS プログラムを紹介する。SAS を実行する手順を示す前
に、ここで利用するデータと出力結果の一部、及びそのための SAS プログラムを
紹介する。
この節は、以下に順に示す2つの例ごとに、つぎの4項から成り立っている:
宿題 A
つぎのデータは、ここでは、心理統計学のテキストの乱数表から取った架空
のデータである。
1 10
1 96
1 26
1 12
1 97
1 18
1 96
1 57
1 15
1 54
1 12
1 48
1 37
1 34
1 65
1 25
1 46
1 45
1 12
1 46
2 10
2 76
2 61
2 15
2 40
2 17
2 14
2 03
2 14
2 55
2 83
2 79
2 20
2 67
2 10
2 75
2 06
2 07
2 98
2 71
|
--- 心理統計学の副読本から取り出した、性による平均の差の検定のための
架空データ例 ---
学生諸君は、この2ページにわたる表の中から、各自の通し番号に対応する箇所
から、縦に見て続けて20個を各ページから取り出し、情報処理教育センターの各自で
ログインした時の z ドライブの下の My Document -> SASUniversityEdition ->
myfolders の下の data フォルダの中に、TeraPad を起動し、
ファイル名 ttest_ex1.txt なる名前をつけてうえの例のように、入力し保存するこ
と。その際、「名前をつけて保存」画面で、ファイル名 の下の
ファイルの種類は「テキストファイル」を選択する こと。
ここで、うえの20個のデータの各行は20人の被験者に対応し、各行とも最初の
1桁の数値が性別(1=男、2=女)を、1つ空白を置き2桁で打ってあるのが、何らか
の心理テストの得点であるとする。もちろん、データはすべて全角ではなく、半角で
入力せよ。
学籍番号に対応する各人のデータの先頭は、各ページごと、左上から右下に向かって
2桁の数値を5つづつ飛ばして到達する位置とする。各列の最後に来たら、次の列の先
頭に戻りカウントすること。
例えば、学籍番号 001 の学生は、p.445 の数値の左最上部の数値から始め、94, 18,
..., 90, 35 までを性別1(男)の20個のデータとし、p.446 の数値の左最上部の数
値 70, 99, ..., 95, 45 までの20個のデータを性別2(女)の20個のデータとし
て、上記データファイルに入力する。
また、例えば学籍番号 012 の学生ならば、p.445 の数値左最上部から2列目の6つ目
の数値から始め、81, 18, ..., 29, 38 を男の20個のデータ、p.446 の数値の左最上
部から2列目の6つ目の数値から始め、96, 62, ..., 29, 61 を女子の20個のデータ
として、データファイルに入力する。
以下の検定結果は、後続の SAS プログラムよって得られたものである。
The TTEST Procedure
Statistics
Lower CL Upper CL Lower CL Upper CL
Variable gender N Mean Mean Mean Std Dev Std Dev Std Dev Std Err Minimum Maximum
x 20 29.187 42.55 55.913 21.713 28.552 41.702 6.3844 10 97
1
x 20 25.9 41.05 56.2 24.617 32.37 47.279 7.2382 3 98
2
x Diff (1-2) -18.04 1.5 21.039 24.943 30.521 39.335 9.6515
T-Tests
Variable Method Variances DF t Value Pr > |t|
x Pooled Equal 38 0.16 0.8773
x Satterthwaite Unequal 37.4 0.16 0.8773
Equality of Variances
Variable Method Num DF Den DF F Value Pr > F
x Folded F 19 19 1.29 0.5897
|
--- 変数 x についての性差の分析の出力結果 ---
うえの出力結果は、その出力順序を含めて注意が必要である。まず最初に見るべき
は、うえの出力の最後の両群の分散の等質性の F-検定結果である。右端の p-値の値
が 0.5897 なので、母分散の等質性の帰無仮説は採択されることがわかる。
ここで、p-値とは、一般に帰無仮説のもとで統計量(この場合、F)が標本での値よ
りも大きな値を取る(理論的な)確率をさす。この検定の場合は、方法(Method) の
項が Folded F となっているので、授業で話した F 値の計算方法、すなわち F 統計
量の分子にいつも分母より大きい値を持ってくるので、そのときの p 値はおよそ
0.295 であるが、理論的には分子が分母より小さいケースの確率も同等量分考える必
要がある。このため、最終的な p 値はこの値の2倍、すなわち、出力結果の Pr > F
の項にある 0.5897 となる。
いずれにせよ、多くのの統計ソフトでは、うえの SAS の出力結
果のように、授業で教えた棄却点の値を数表から読む必要はなく、そのかわりに帰無仮
説の検定の危険率(1% とか5% など)は、p 値を見るだけで、帰無仮説の採択・棄
却を判断することができるのである。
ただし、テキスト p.24 で述べた理由により、
- 両群の分散が等しいとみなされる場合
分散の等質性の検定と平均の差の検定を経時的に行う時は、全体の危険率の
インフレが生じるので、両検定がこの場合独立になることを用いると、個々の
検定の危険率は、全体の危険率を5%水準に抑えたければおよそ 2.5% に、同
じく1%水準に抑えたければおよそ 0.5% にする必要がある。
- 両群の分散が等しいとみなされない場合
この場合、平均の差の検定そのものに無理があるとも見れるが、ここでは
通常のテキストにあるように検定はおこなうものとする。また、この場合、全体
の危険率の計算は困難であるので、分散の等質性の検定の危険率はうえの方式
で行うものの、平均の差の検定に際しては分散が等しいとみなされる場合の
ような危険率のコントロールは行わず、とりあえず通常の単独での危険率(例え
ば5%とか1%とか)で行うこととする。
いずれにせよ、その結果からは、両群の平均の差の検定において、われわれは母
集団の分散が等しい場合の通常の t-検定を選択する必要がある。そのためにはわれ
われは、うえの出力結果の中段の T-Tests の項で、Method として Satterthwaite
の方法でなく、Pooled すなわち通常の t-検定の項を見ないといけない。言い換え
れば、このデータでは、分散が等質な場合、すなわち Variances の項で Equal と表
示されている行の t-値や p-値を見る必要があることに注意したい。これに対応する、
右端の p-値の値は 0.8773 となっており、上の議論から、全体の危険率が5%の
場合0.025 より大きいので、また同危険率が1%の場合 0.005 より大きいので、
どちらで検定する場合も母平均の差がないという帰無仮説は採択されることがわかる。
最後に、われわれはうえの出力結果のうちの最上段のデータの基礎情報を見ること
になる。各群でサンプル数の右側には、まず各群の母平均の信頼区間(信頼度を何も
指定しない場合、信頼度は 0.95 である)の下限値、標本平均 (Mean)、同信頼区間
の上限値が並んでいる。つぎに、その右側には同母標準偏差の信頼下限値、標本
不偏標準偏差 (Std Dev)、同母標準偏差の信頼上限値、標準誤差、標本の最大値、同
最小値と続く。
ここで、注意すべきは SAS では、ここでの Std Dev は、標本
標準偏差ではなく、標本不偏標準偏差である点である。このプロシジャには、この値
を標本標準偏差に変えるオプションはついていない。そこで、諸君は、SAS で出力さ
れている x と y ごとの(標本)不偏標準偏差(これを、一般的に su と
書くことにする)を、つぎの関係式を用いて(標本)標準偏差 sxや
syに、変換しないと、授業中に計算した諸君の標準偏差とは一致しない
ので注意せよ。つぎの例は、x の(標本)標準偏差の計算式である。y についても同様
である。ここで、sqrt [...] は、[...] の平方根を表すものとする。また、N は x
グループや y グループのサンプル数で、授業では 20 か 10 であった:
sx = sqrt[(N-1)/N}*su

上記のような少数データの出力結果を手にするためには、SAS の場合、まずデータ
に変数情報等を付けて特定のフォルダに保存しておくことはせず、つぎのプログラム
にあるように、データをうえのようにあらかじめ p ドライブの data なるフォルダ
の下に名前をつけて(ここでは、ttest_ex1.txt なる名前)保存しておいたものを、
呼び出して、以下のような変数情報をつけて一時的ファイルとし、それを ttest プ
ロシジャで分析するのが簡単である。以下には、そのための SAS プログラムを示し
た。
(1) 平成28年度から導入された SAS 無償バージョン用のプログラム
*-------------------------------------------------------------------------*
| February 2, 2016 |
| |
| a sasprogram for testing the difference in means of two groups. |
| |
*-------------------------------------------------------------------------*;
filename data '/folders/myfolders/data/ttest_ex1.txt';
options ps=60;
data work;
infile data;
input gender 1. x 3.;
label gender='gender of subject/1=male, 2=female'
x='mark of a test';
run;
title 'gender difference in a psychological test';
proc ttest data=work;
class gender;
var x;
run;
|
--- 架空データを用いた、2群の平均の差の検定のためのプログラム (SAS 無償バージョン用)---

(2) 平成27年度まで導入されていた SAS バージョン 9.4 等でのプログラム
*-------------------------------------------------------------------------*
| October 6, 2004 |
| |
| a sasprogram for testing the difference in means of two groups. |
| |
*-------------------------------------------------------------------------*;
filename data 'p:\data\ttest_ex1.txt';
options ps=60;
data work;
infile data;
input gender 1. x 3.;
label gender='gender of subject/1=male, 2=female'
x='mark of a test';
run;
title 'gender difference in a psychological test';
proc ttest data=work;
class gender;
var x;
run;
|
--- 架空データを用いた、2群の平均の差の検定のためのプログラム ---

以下のプログラムと具体的手順は、平成28年度からの SAS 無償バージ
ョン用のものである。

- TeraPad を起動し、授業中に実習した、自分の学籍に対応する10個
のデータを z ドライブ -> My Documents -> SASUniversityEdition -> myfolders
-> の下の data フォルダに入力し、ttest_ex1.txt なる名前で保存する。
保存時に、うえのデータ例のところに書いたように、ファイ
ルの種類を間違えないように注意せよ。
- インターネットエクスプローラ (IE) を開き、千野のホームページの
うえのダウンロードコーナーからプログラムを
z ドライブ -> My Documents -> SASUniversityEdition -> myfolders の下の
sasprog フォルダに保存する。
- デスクトップ画面から SASUniversity Edition を起動し、所定の手順に従い、
デスクトップ上に SAS Studio なる画面を表示させる。
- その後の手順については、春学期授業の最初に配布するウエブ操作に関する
ファイルを参照のこと。

宿題 B
データ例2 は、
今泉 (1991) が収集した54名の被験者の筆跡と性格に関するものである。概要に
ついては3.4.2 節を参照のこと。
以下の検定結果は、後続の SAS プログラムの一部である ttest
プロシジャによって得られたものである。詳細は、上記 3.4.2 節の中の
「男性役割5因子の性差の分析のためのプログラムの出力結果の見方」の項をクリックし
参照のこと。
TTEST PROCEDURE
Variable: FACTOR1
GENDER N Mean Std Dev Std Error
----------------------------------------------------------------------
1 14 -0.43951104 1.15235295 0.30797928
2 40 0.15382886 0.84347227 0.13336468
Variances T DF Prob>|T|
---------------------------------------
Unequal -1.7679 18.1 0.0939
Equal -2.0538 52.0 0.0450
For H0: Variances are equal, F' = 1.87 DF = (13,39) Prob>F' = 0.1327
|
--- 男性役割5因子についての性差の分析の出力結果の見方 ---

上記のような出力結果を手にするためには、SAS の場合、まず今泉データに変数
情報等を付けて特定のフォルダに保存しておくと便利である。そのようなファイル
は、SAS では「永久 SAS ファイル」と呼ばれる。以下には、そのための SAS プロ
グラムを示した。
プログラムの詳細については、3.4.2 節の
筆跡・性役割データの
永久 SAS ファイル化の項を参照のこと。
filename yumidata '/home/shinri/chino/educdata/thesis/p88014yi';
libname permfile '/home/shinri/chino/sasset/multivar';
options pagesize=60;
data permfile.yumi;
infile yumidata;
input noss 2. +1 gender 1. +1 (rolm1-rolm29) (1.) +1
(rolf1-rolf29) (1.) mfi 4. +1 ratio 3.1
/+4 (hola1-hola28) (1.)
/+4 (holb1-holb28) (1.)
/+4 (holc1-holc28) (1.)
/+4 (hold1-hold28) (1.)
/+4 (hole1-hole28) (1.);
label noss='sample number'
gender='gender of subjects'
mfi='muscularity-feminity index'
ratio='correct judge of gender';
run;
libname library '/home/shinri/chino/sasset/format';
proc format library=library;
value sexfmt 1='male' 2='female';
run;
proc print data=permfile.yumi n;
title 'thesis data by p88014, Yumi Imaizumi';
run;
|
--- 今泉 (1991) データの永久SASファイル化 ---
SAS プログラムの基本的な約束事に関しては、筆者の講義ノートの中の「データ
解析/基礎と応用」の
目次
の下方の「付録 SAS プログラムの作成」の項を参照されたい。
一旦、上記のような永久 SAS ファイルが特定のフォルダに作成されたなら
ば、我々は、以下のような数行の SAS プログラムによりいろいろな検定や計算
をすることができる。下記のプログラムのうち、上述の t-検定の結果を出力す
るための部分は、proc ttest ... 以下の4行に過ぎない。
プログラムの詳細については、
を参照のこと。
libname permfile '/home/shinri/chino/sasset/multivar';
options pagesize=60;
title 'principal FA for Imaizumi data/ 5-factor solution';
proc factor data=permfile.yumi
nocorr priors=s n=5 r=v re score outstat=factout;
var rolm1-rolm29;
run;
proc score data=permfile.yumi score=factout out=scores;
run;
title 'gender differences in each of the five factors';
proc ttest data=scores;
class gender;
var factor1-factor5;
run;
proc sort data=scores;
by gender;
run;
options pagesize=40;
title 'histogram of each of the five factors by gender';
proc chart data=scores;
by gender;
vbar factor1-factor5;
run;
options pagesize=60;
title 'normality test for each factor by gender';
proc univariate data=scores normal;
by gender;
var factor1-factor5;
run;
|
--- 男性役割5因子についての性差の分析のためのプログラム ---

- インターネットエクスプローラ (IE) を開き、千野のホームページの必要
箇所からデータ (p88014yi なるファイル名のファイル)及び2つの SAS
プログラム(perm_yi.sas 及び fact_dif.sas なるファイル名のファイル)
を Pドライブの下に保存する
- まずデータ (p88014yi) をダウンロード
ダウンロードは、筆者のホームページのテキスト「データ解析/基礎
と応用」の中の、「第3章 因子分析」の中の「3.4.2 節 筆跡・性
役割データへの適用例」の、先頭の目次の項の「1. 筆跡・性役割データ
の永久 SAS ファイル化」をクリックし、その項の先頭の文章中の
「つぎのデータは、...」の「データ」部分をクリックし、やはり
筆者のホームページの中のテキスト「心理統計学」の第2章で既に
やったと同じ手順で、データを p ドライブの Report フォルダ
(マイコンピュータ -> P ドライブ -> letter -> chino -> psychomet
-> Report とクリック) の下の、各自の学籍番号から成るフォルダの
直下の既に作成済みの data フォルダの下に保存する。
- つぎに、1つ目の SAS プログラム (perm_yi.sas) をダウンロード
この場合、フォルダは p ドライブの Report フォルダの下の、各自
の学籍番号から成るフォルダの直下の既に作成済みの sasprog フォルダ
であることに注意せよ。
- つぎに、2つ目の SAS プログラム (fact_dif.sas) をダウンロード
この場合も、フォルダは p ドライブの Report フォルダの下の、各自
の学籍番号から成るフォルダの直下の既に作成済みの sasprog フォルダ
であることに注意せよ。
- SAS を起動し、プログラムエディタ上に 2. で保存した2つの SAS プ
ログラム (perm_yi.sas、fact_dif.sas)を、以下の手順で1つ読み込ん
では修正し実行、2つ目も同様にする
- 1つ目のプログラム (perm_yi.sas) を修正し、実行する
ここで、このプログラムの場合、修正すべき個所は、最初の2行に
おける引用符内を第2章のところで行ったと同様な修正をするだけで
なく、同プログラムの最後から7行目の libname 文の中の引用符内
の最後の format のみを残し同様に修正しないといけないので注意せよ。
もちろん、最初の1行目の filename 文における引用符内の最後の
ファイル名 p88014yi は残さないといけない。
- 2つ目のプログラム (fact_dif.sas) を修正し、実行する
修正手順は、上記 perm_yi.sas と同様であるので詳細は
省略する。もちろん、この場合、修正個所は最初の1行目のみ
である。
- 2つ目のプログラムの出力結果の保存
2つ目のプログラムの実行が正常終了し出力結果が output ウインドウ
に表示されたならば、第2章の場合と同様、sasout に fact_dif.lst
なる名前をつけてそれを保存する。


脚注
脚注1 : 通し番号は新1年生は学籍番号の下3桁、それ以外
の学生は第1回目の授業の時決められものを用いること
脚注2 : 小数点は、同一列内の数字 3 と 8
をダブルマークせよ

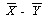 の標本分布は、平均及び分散
の標本分布は、平均及び分散
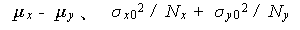
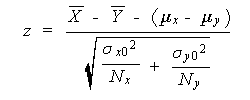
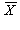 と
と 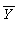 を標本の値
を標本の値
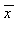 及び
及び 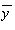 に置き換えて、
に置き換えて、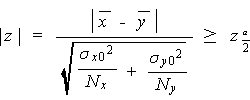
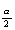 は、
第3章の (3.13) 式で既に学んだ標準正規分布の上側
100
は、
第3章の (3.13) 式で既に学んだ標準正規分布の上側
100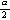 パーセント点である。
パーセント点である。
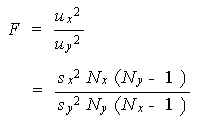
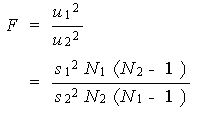
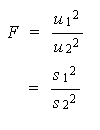
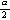 パーセントで
パーセントで
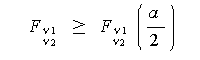
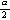 パーセント点
の値である。例えば、検定の危険率を α =0.05 すなわち、5 パーセント
水準とするならば、この値は、右側 2.5 パーセント点である。通常の F -分布表
では、危険率が5パーセントか1パーセントの場合しか載っていないので、このような
半端な値の場合は通常のF -分布表では、したがって岩原のテキスト末尾の数表でも、
見ることができない。
パーセント点
の値である。例えば、検定の危険率を α =0.05 すなわち、5 パーセント
水準とするならば、この値は、右側 2.5 パーセント点である。通常の F -分布表
では、危険率が5パーセントか1パーセントの場合しか載っていないので、このような
半端な値の場合は通常のF -分布表では、したがって岩原のテキスト末尾の数表でも、
見ることができない。
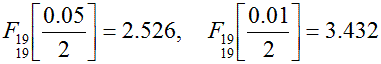
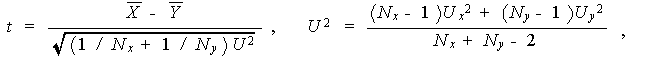
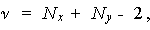
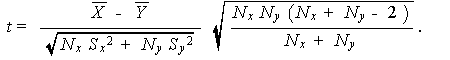
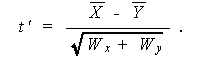
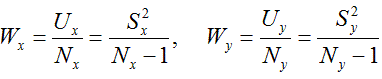
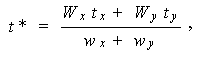
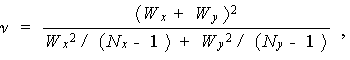
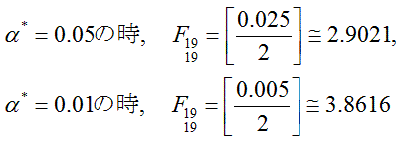

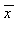 、及び
、及び
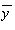 を求める。
を求める。
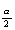 の値は、問題用紙で指定
された危険率に対応するものを選ばねばならないことに注意せよ)。
の値は、問題用紙で指定
された危険率に対応するものを選ばねばならないことに注意せよ)。
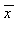 、
及び
、
及び 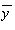 を求める。
を求める。
![]()
![]()
![]()
![]()
![]()