このページは、平成11年6月7日に開設した。
このページは、令和2年4月24日に一部更新した。
![]()
1.1 事象
統計学では、実験や観測結果のことを 事象 (event) と呼ぶ。例えば、 さいころを投げると、1から6の目のいずれかが出るが、それぞれは1つの事象 である。
事象 E に対して、E が起こらないという事象を E の
余事象 (complementary event) と呼ぶ。「2つの事象 E1 と
E2 が同時に起こる」という事象は
E1
E2
と表される。
これに対して、「2つの事象 E1 と E2 のいずれかが起こる」という事象は、
E1
E2
と表される。また、同時に2つの事象 E1 と
E2 が起こることが決してない時、E1 と E2 は
排反的 (exclusive) と呼ばれる。また、「事象 E1 が起これば
必ず事象 E2 も起こる」ということを、
E1
E2
と書く。この時、集合論では E1 は E2 の
部分集合 (subset) であるという。
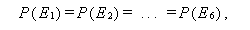
|
(1) |
である。
ここで、一般に起こりうるすべての異なる数の集合から成る事象を 標本 空間 (sample space) と呼ぶことがある。さいころの場合、それは 1,2,3, 4,5,6 である。これを Ω と表せば、一般に P(Ω)=1 である。
確率をより正確に定義すると、つぎのようになる:
一般に、標本空間 Ω は、さいころのような整数値を取る場合と、実数値 を取る場合がある。
このようにして定義される確率は、標本空間またはその部分集合に対して定義 できるので、一種の変数(変量)とみなすことができる。つまり、確率を標本空間 の部分集合の関数とみなす時、われわれはこれを 確率変数 (random variable) と呼ぶ。
一般に2つの事象 E1、E2に対して
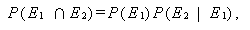
|
(2) |
が成り立つ。したがって、
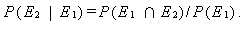
|
(3) |
上の式での P (E2 | E1) を、E1 のもとでの E2 の 条件付 確率 (conditional probability) という。(2) 式及び (3) 式とも、 E1 と E2 を交換すると、つぎの式が成り立つ:
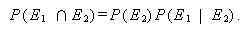
|
(4) |
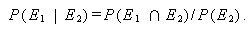
|
(5) |
もし、(2) 式で P (E2 | E1) が P (E2) に等しい時は、
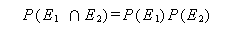
|
(6) |
が成り立つ。この時、2つの事象は 独立 (independent) という。
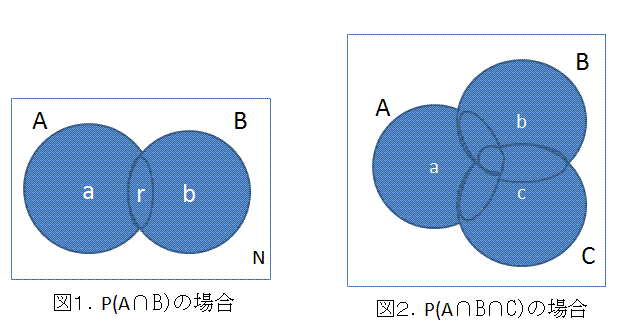
確率不等式(probability inequalities) 全般にわたる専門的な解説書の1つに Tong (1980) がある。例えば、多変量正規分布、多変量 t 分布、多変量カイ2乗分布、 多変量 F 分布、などは、それらのうちの1群である。この節では、各種確率不等式のうち、 分布によらない不等式(distribution-free inequalities) の中の基本的なものに ついてまとめる。これらは、分散分析における多重比較において、よく利用される。ただし、最初の「ブール の公式」は、不等式ではなく等式であることに注意せよ。
これについては、Hochberg & Tamhane (1987, p.363) が詳しい。それによれば、
E1, E2, ... , Ek,
k2
を確率事象(random events) とし、Eic
を事象 Eiの補集合(complement) とする時、
|
をブールの公式(又は、ポアンカレの公式)という。
 |
|
例えば Hochberg & Tamhane (1987) も指摘しているように、よく知られた ボンフェロニ不等式は、上記ブールの公式(I.1) 式の 一次近似(the first order approximation) を用いるもので、
|
 |
が成り立つので、
あるいは、
|
とも書ける。こちらの不等式の方が、分散分析の対比検定(とりわけ、計画的非直交対比に対する 対比検定)における実験当たりの過誤率αEW の上限値 (n upper bound) を与えるボンフェロニ不等式の 原型を与える式としては、直接的で理解しやすい。例えば、(I.5)式で、Ai は、 i 番目の対比検定で帰無仮説が棄却されるという事象とみなし、個々の対比検定の危険率がすべて 一定でαである、と仮定すれば、この式は対比検定におけるよく知られたボンフェロニ不等式その ものであることは、明らか。なお、(I.4)式の表現は、Hsu (1996, p.228)と同一。
あるいは、
|
|
あるいは、
|
(AI.8)式あるいは(AI.9)式の不等式の特徴は、
P(Ai)
の上限値を構成する式の最後の係数が必ず正になる項
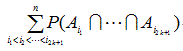 |
を含むという点であり、不等式は自明。
つまり、(AI.8)式または(I.9)式は、ブールの公式の右辺の任意の偶数項(ただし、
-1 のべき乗のベキは奇数)までの和が
P(Ai)
の下限値に、同じくその偶数項の次の項(ただし、-1 のベキは偶数)までの和が
P(
Ai)
の上限値を示す式といえる。(I.8)式は誰が提案した式かは、統計学辞典には書かれていない。
(I.3) 式のブールの公式の一次近似を同時2変量確率のみを用いてさらに改良したものが、 クニア(Kounias, 1968) により提案されている:
あるいは、
|
うえの式は、次のようにも書ける:
|
Tong (1980, p.147) の次の不等式は、クニアの不等式での
P(Ei
c)の下限値についても加えたものである:
|
Hochberg & Tamhane (1987)によれば、クニアの不等式はその後 Hunter (1976) 及び
Worsley (1982) が独立に同じ結果を得た。以下の結果は、グラフ理論
(the graph theory) に基づく。ここで、サイクル(cycle) を持た
ない連結グラフ (the connected graph)、すなわち
生成木 (the spanning tree) を T としよう。この時、もし T が頂点{1, ..., P}を
を持つ生成木であり、かつ
{i, j}T は
i と j が隣接している (djacent) ことを表すならば、次の不等式
が成り立つ:
|
上式の最も精確な限界値は、右辺第2項が最大になるような生成木を見つけることにより得られる。 この問題を解くには、Kruscal (1956) の最小生成木アルゴリズム (the minimal spanning tree algorithm) を用いればよい(Hochberg & Tamhane, 1987, p.364)。
2.1 度数分布・母集団分布・標本分布
われわれが手にする (観測する) データは、それらが1変量であれ多変量であれ、 観測対象となる数値の集まり (これを、統計学では 母集団 (population) と 呼ぶ) の中から抽出される。ここで、対象となる母集団の数値の数が有限である 場合、 有限母集団 (finite population)、無限である場合、 無限 母集団 (infinite population) と呼ばれる。
また、抽出された N 個のデータは、サイズ (大きさ) N の 標本 (sample) と呼ばれる。
標本抽出の仕方についての2つの重要な概念に、復元・非復元、及び作為・無作為 がある。前者は、サイズ N の標本を選るに際して、一度抽出した個体を戻すか どうかで、戻さない抽出法を 非復元抽出 (sample without replacement)、 戻した後再度抽出する方法を 復元抽出 (sample with replacement) と それぞれ呼ぶ。
後者は、標本抽出を作為的に行うかどうかで、統計学の理論は 無作為抽出 (random sampling) による 無作為標本 (random sample) を前提にする。
さて、母集団での数値の集まりの特徴を見るためには、それらの値のそれぞれを 取る度数なり確率がどれだけあるかがわかればよい。それぞれの数値を横軸に取り、 対応する度数なり確率を縦軸にして、数値のばらつき具合を示したものは、 母集団分布 (population distribution) と呼ばれる。
有限母集団であれば、時間と費用をいとわなければ全数抽出すれば母集団分布は 正確に得られるが、多くの場合それは不可能で、母集団から適当なサイズの標本を 抽出し、それについての分布を描き母集団分布の特徴を推論する。
いずれにせよ、サイズ N の標本における数値を横軸に、度数を縦軸に取って、 数値のばらつき具合を示したものを、 度数分布 (frequency distribution) と呼び、通常母集団分布と区別する。
最後に、統計学ではこれらの他に、 標本分布 (sampling distribution) なる
概念も用いる。例えば、ある母集団からのサイズ N の標本を1つ得たとする。
また、その平均値を  とする。
この
とする。
この  は、異なる標本では
一般に異なる値を取る。つまり、
は、異なる標本では
一般に異なる値を取る。つまり、 は標本を変
えると、同一母集団からからの標本であるにもかかわらずいろいろな値を取る、すなわちある分布を持つ
ことになる。通常標本平均は定数と考えるが、上の意味では定数ではなく確率変数とも考えることができ
る。そこでそのような場合、われわれは
は標本を変
えると、同一母集団からからの標本であるにもかかわらずいろいろな値を取る、すなわちある分布を持つ
ことになる。通常標本平均は定数と考えるが、上の意味では定数ではなく確率変数とも考えることができ
る。そこでそのような場合、われわれは 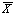 と書き、
と書き、
 と区別する。一般に、
と区別する。一般に、
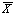 のように標本から作られる量を
統計量 (statistic) と呼ぶ。また、その分布は標本分布と呼ばれ、上述の度数分
布や母集団分布と区別する。
のように標本から作られる量を
統計量 (statistic) と呼ぶ。また、その分布は標本分布と呼ばれ、上述の度数分
布や母集団分布と区別する。
われわれが手にする度数分布は、前節から明らかなように多くの場合、何らかの 母集団分布からのサイズ N の無作為標本とみなされるが、母集団の 理論分布 (theoretical distribution) としては、これまでに多くの分布が提案されている。 これらの分布は、いろいろな角度からの分類が可能であるが、1つの方法は分布を 離散的分布 (discrete distribution) と 連続分布 (continuous distribution) とに分類することである。離散的分布とは、標本空間の要素がさいころ の目の場合のように飛び飛びの値を取る場合であり、連続分布とは、それらが連続 的な値を取る場合である。離散的分布としては、 2項分布 (binomial distribution)、 多項分布 (multinomial distribution)、 ポアソン分布 (Poisson distribution) などが、また連続分布としては、 正規分布 (normal distribution)、 F-分布 (F-distribution)、 t-分布 (t-distribution)、 χ2-分布 (chi-square distribution)、 などがよく知られている。
如何なる確率変数 X の分布も、分布が離散的であれ連続的であれ、標本空 間の各要素に対する確率が特定できれば決まる。そこで、これを
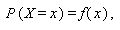
|
(21) |
と書くものとする。この式の f (x) を確率変数が離散型の時には単に 確率関数 (probability function) と、連続型の時には 確率変数 X の 確率密度関数 (probability density function) と呼ぶ。 確率密度関数は、 確率密度 (probability density) あるいは単に 密度 (density) と呼ばれることもある。
一般に、f(x) が確率関数、すなわち離散型の関数、の場合には、f(x) の値が1を超える ことはないが、f(x) が確率密度(関数)の場合には、分布によっては確 率密度 f(x) は x のある範囲では1を超えることがある。F-分布、カイ2乗分布、指数 分布やベータ分布は、そのような例である。しかし、 1.2 節で述べた「確率」の定義での事象に あたるものは任意の連続分布の場合、特定の値 x ではなく特定の範囲(a 以上 b 以下)であり、 x が特定の値を取る確率密度がたとえ1を超える値を持つ分布の場合でも、x が特定の範囲に入 る確率は1を超えることはないので、 1.2 節の確率の定義に矛盾しない。以下に、MATLAB に よる上記の分布のうち、F-分布及びベータ分布の確率密度関数の例を示す。
まず、図3は自由度の異なるF-分布の確率密度関数の例を4つ示す。
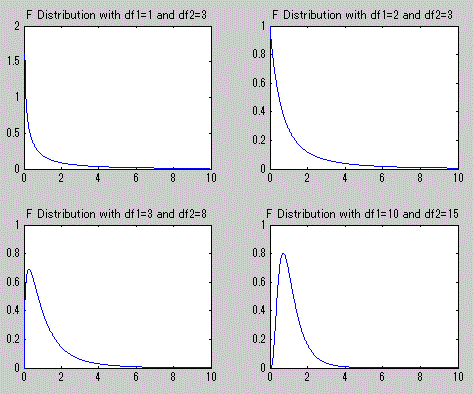
図3. F-分布の確率密度関数の例
つぎの図4は、2つのパラメータ (a, b) を (0.5, 0.5) (赤)、(3, 3) (緑)、(3, 1) (青)、
(1, 3) (星形5角形)、(2, 6) (黒)、(6, 2)(マゼンタ)と変えた場合の
ベータ分布の確率密度関数の例を示す。これを見ると、ベータ分布は非常に多くの形をし
た分布が含まれることがわかる。
とりわけ、心理学でよく使われる5件法や7件法を用いた評定尺度データの分布では正の歪度(
分布の右側により長い尾を持つ)を持つ分布や、逆に負の歪度(同左側により長い尾を持つ)分布
の近似にも使えそうな分布も含まれることに注意したい。また、心理学の領域のデータの場合、
ときどき赤色で示した分布のように U 字型となるものもみられるが、ベータ分布はこれにも対応
できることは興味深い。
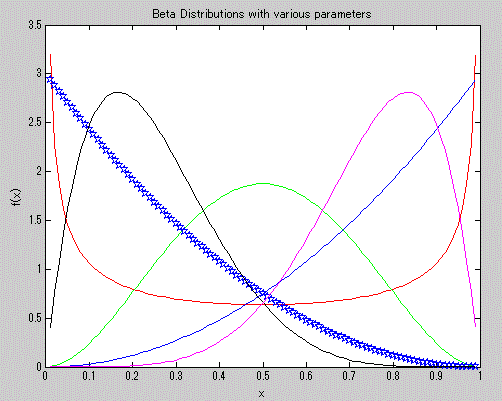
図4. ベータ分布の確率密度関数の例
一方、X が離散型か連続型かにより、
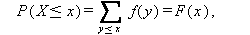
|
(22) |
または、
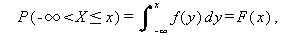
|
(23) |
なる関数を、 累積分布関数 (cumulative distribution function) もしくは 単に 分布関数 (distribution function) と呼ぶ。例えば、連続 分布の1つとしてよく知られた正規分布の確率密度(または密度関数)、及び 分布関数は、それぞれつぎのように書ける。ここで、正規分布の形を決める パラメータである平均値と分散は、それぞれ μ 及び σ2 であるとする:
まず、正規分布の確率密度関数は、
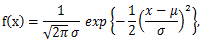
|
(24) |
である。ここで、正規分布はしばしば平均 μ と分散 σ2 を用いて、 N(μ, σ2) と 表記される。図5は正規分布の確率密度関数の幾つかの例を 示したものである。
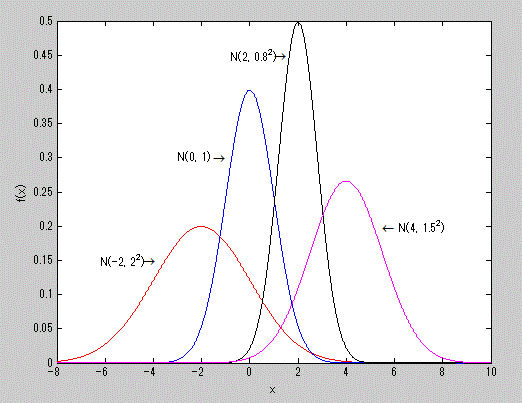
図5. 正規分布の確率密度関数の例
一方、正規分布の分布関数は、
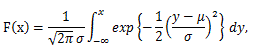
|
(25) |
である。また、正規分布 N(4, 1.52) の分布関数における x=3 までの累積 密度を青色で塗りつぶして示したのが図6である。
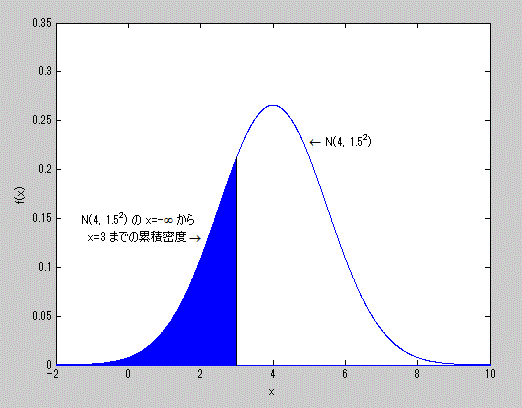
図6. 正規分布の分布関数による累積密度の例
確率変数 X の分布の特徴を表すための最も基本的な指標に、 期待値 (expectation) 及び 分散 (variance) がある。前者の期待値は平均値 とも呼ばれ、X が離散型か連続型かにより、それぞれ

|
(26) |
または、
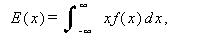
|
(27) |
として定義される。
期待値については、つぎのような性質がある:
|
後者の分散は、X が離散型か連続型かにより、つぎのように定義される。 ここで、E (X)=μ とする:

|
(31) |
または、
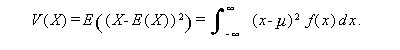
|
(32) |
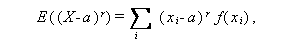
|
(33) |
または、
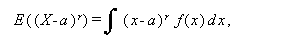
|
(34) |
分散については、つぎのような基本的な性質がある:
|
最後の不等式は、 チェビシェフの不等式 (Chebyshev's inequality) と 呼ばれる。
最後に、統計学的分布の特徴として、平均、分散と並び時々議論されるものに、分布の
歪度 (skewness) と 尖度
(kurtosis) がある。歪度は分布の対称性からの歪みを、尖度は分布の(正規分布に比べての)
尖がり具合を、それぞれ表す。
まず、歪度を γ1 と表すとして、
と定義される。ここで、μ2、μ3 は、
それぞれ、平均の周りの2次、及び3次の積率である。ちなみに、正規分布の場合、
μ2 = σ2、μ3 = 0 なので、
γ1 = 0 である。また、歪度は、定義から μ3 と同符号なので、
歪度 γ1 が正の分布では、分布はその右側に長い裾を持つ分布となるの
に対して、歪度が負の分布では、分布はその左側に長い裾を持つ分布となることがわかる。
一方、尖度を γ2 と表すとして、
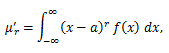
|
(38) |
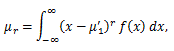
|
(39) |
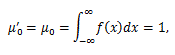
|
(40) |
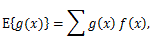
|
(41) |
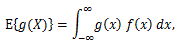
|
(42) |
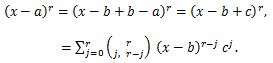
|
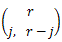
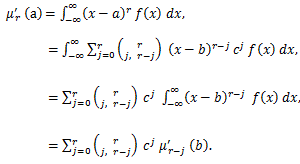
|
(1) b=μ'1 ならば、a=0 として、
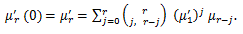
|
(43) |
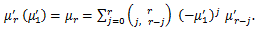
|
(44) |
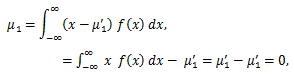
|
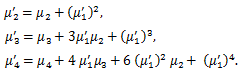
|
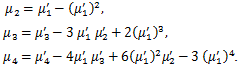
|
(45) |
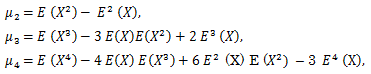
|
(46) |
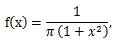
|
(47) |
|
(48) |
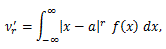
|
(49) |
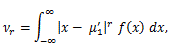
|
(50) |

|
(51) |
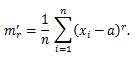
|
(52) |
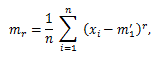
|
(53) |
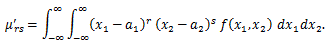
|
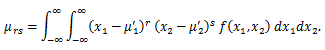
|

|
(54) |
確率母関数については、つぎのことが言える:
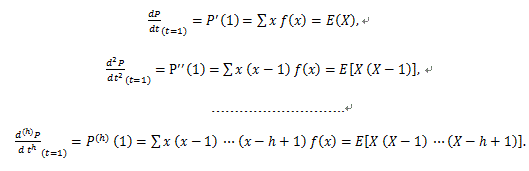
|
(55) |
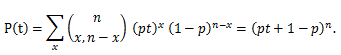
|
(56) |
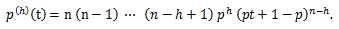
|
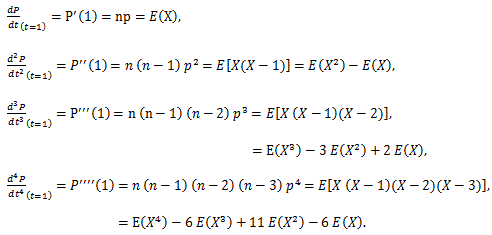
|
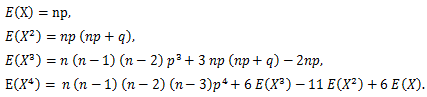
|
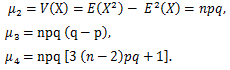
|
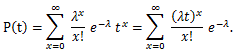
|
(57) |
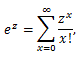
|
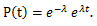
|
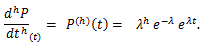
|
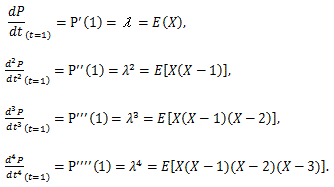
|
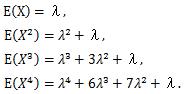
|
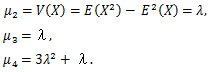
|
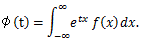
|
(58) |
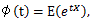
|
(59) |
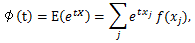
|
(60) |
|
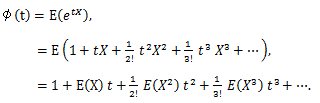
|
(62) |
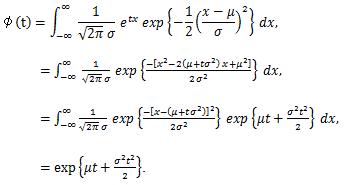
|
(63) |
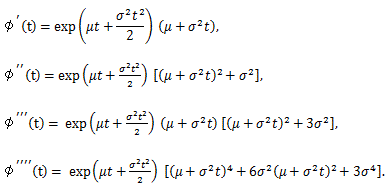
|
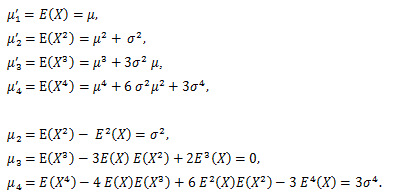
|
|
|
性質3を用いると、次の定理を証明できる:
の分布は、n が無限大の時、正規分布 N(0, 1) に収束する。 |
Y の積率母関数 φn(t) は、
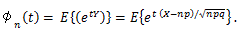
|
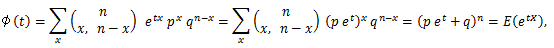
|

|
そこで、
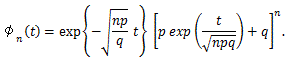
|
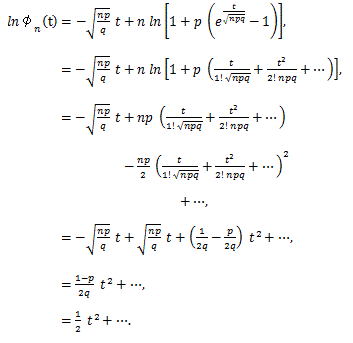
|
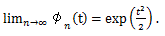
|
積率母関数は、t の幾つかのあるいはすべての値に対して存在しなことが多い。そこで、より 一般的な形の関数を用いることがある。それが、次節の特性関数である。
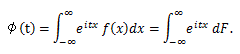
|
(65) |
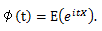
|
(66) |
.gif)
|
(67) |
一般に、特性関数の絶対値は上式の性質から
|

|
(69) |
は収束するので、つぎの性質がある:
|
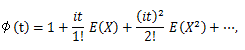
|
(70) |
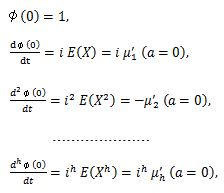
|
(71) |
|
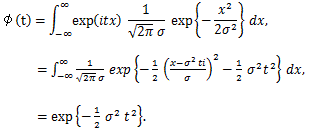
|
(73) |
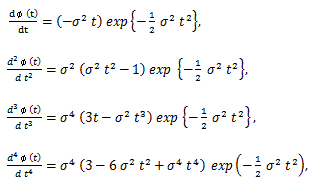
|
(74) |

|
(75) |
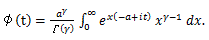
|
(76) |
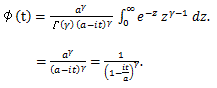
|
(77) |

|
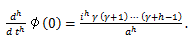
|
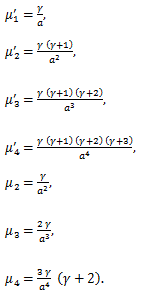
|
(78) |
|
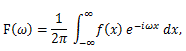
|
(79) |
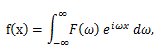
|
(80) |
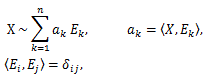
|
(81) |
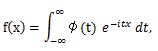
|
(82) |
.gif)
|
(83) |
まず、2変量乗積積率の特性関数はつぎのようになる:
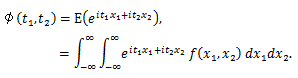
|
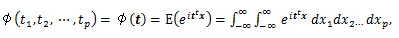
|
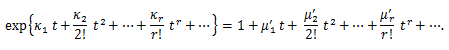
|
(84) |
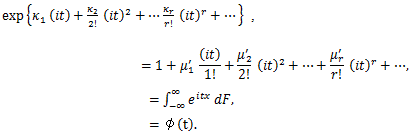
|
(85) |
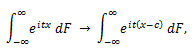
|
|
|
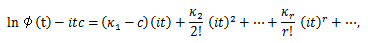
|
積率とキュミュラントの関係は、(84) より、
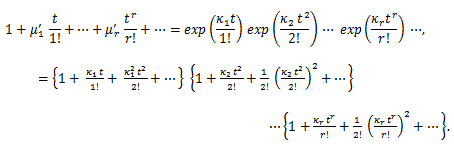
|
(86) |
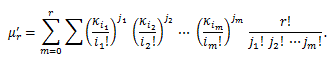
|
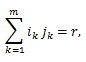
|
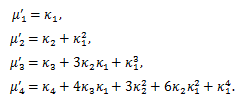
|
(87) |
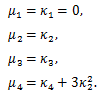
|
(88) |
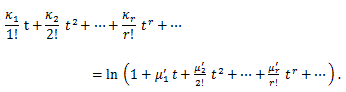
|
.gif)
|
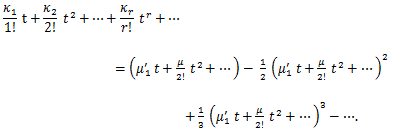
|
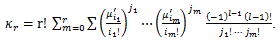
|
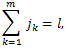
|
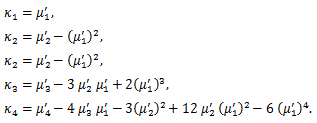
|
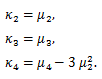
|
(89) |
|
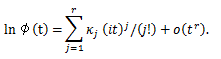
|
(90) |

|
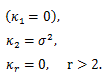
|
(91) |
|
|
|
|
μ'1 = E (X)=μ、μ2 = V (X) = σ2、μ3 = 0、 μ4 = 3 σ4、γ1 = 0, γ2 = 0.
|
|
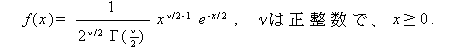
|
(93) |

|
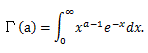
|
|
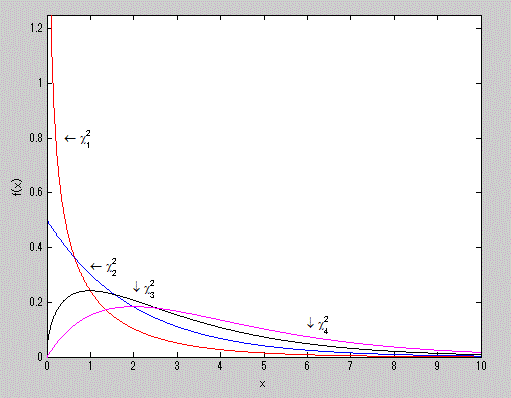
図7. χ2-分布の確率密度関数の例
μ'1 = E (X)=ν、μ2 = V (X) = 2 ν、μ3 = 8 ν、μ4 = 12 ν (ν + 4)、γ1 = 2 21/2 /ν1/2, γ2 = 12/ν.
|

|
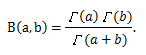
|

図8. F-分布の確率密度関数の例
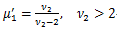
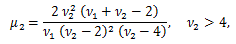
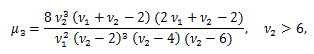
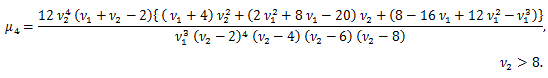
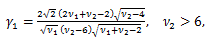
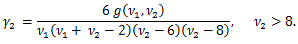
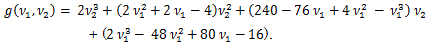
|
|
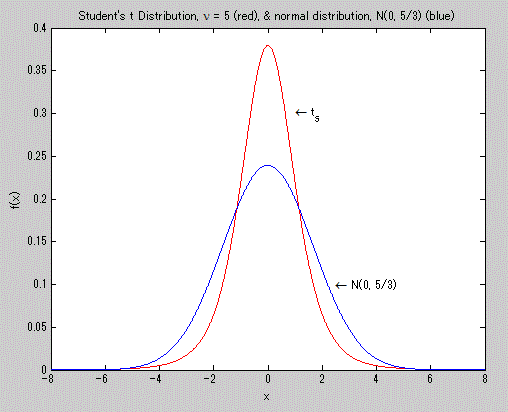
図9. t-分布の確率密度関数(赤色)の例(青色は正規分布の例)
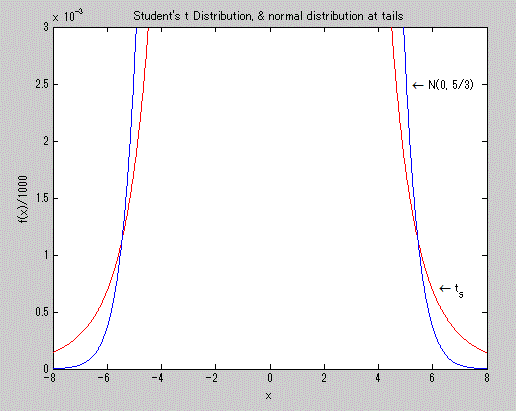
図10. t-分布の確率密度関数(赤色)(青色は正規分布の例)の尾の部分の特徴
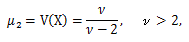
μ3 = 0,
γ1 = 0,
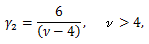
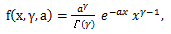
|
(62) |
|
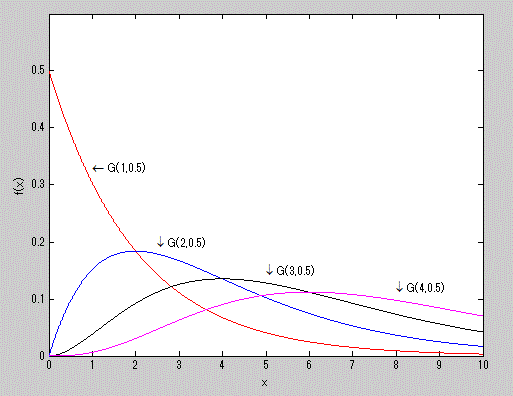
図11. ガンマ分布の確率密度関数の例
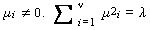 に従う変数の2乗和の分布として
定義される。ここで、λ をこの分布の 非心母数
(non-central parameter) と呼ぶ。
に従う変数の2乗和の分布として
定義される。ここで、λ をこの分布の 非心母数
(non-central parameter) と呼ぶ。
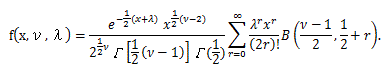
|
(97) |
ここで、ν は正整数であり、λ 0,
z
0 である。非心 χ2 分布で
非心母数の値がゼロの場合が、上述の χ2 分布であることは、非心 χ2
分布の定義式である (43) 式と、χ2 分布の定義式である (40) 式を比較するに際して、
上述の F-分布の定義のところで定義した
ベータ関数
とその性質に注意すれば、明らかとなる。
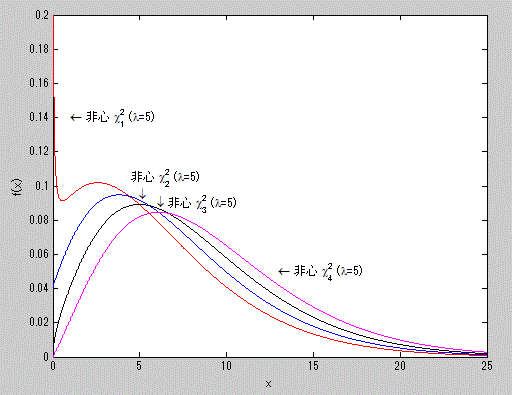
図11. 非心度 λ=5.0 の非心 χ2-分布の確率密度関数の例
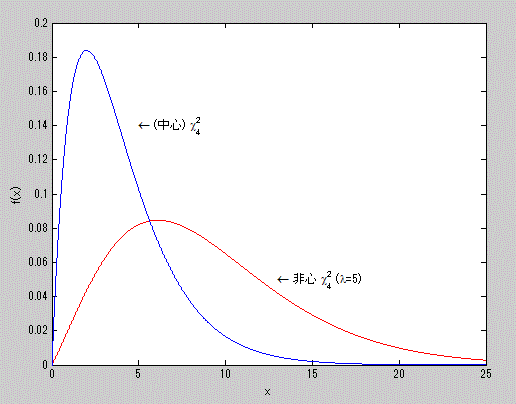
図12. (中心)χ2-分布と非心 χ2-分布の確率密度関数の比較

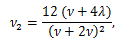
これらより、同分布は常に正の歪度を持つ分布で、急尖分布であることがわかる。
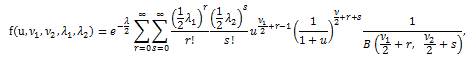
|
(98) |
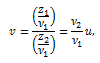
|
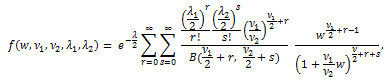
|
(99) |
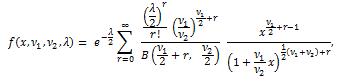
|
(100) |
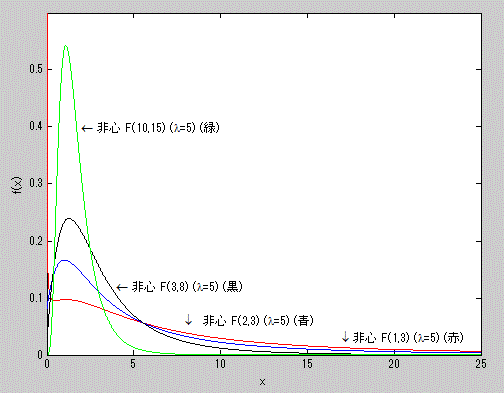
図13. 非心度5の非心 F-分布の確率密度関数の例
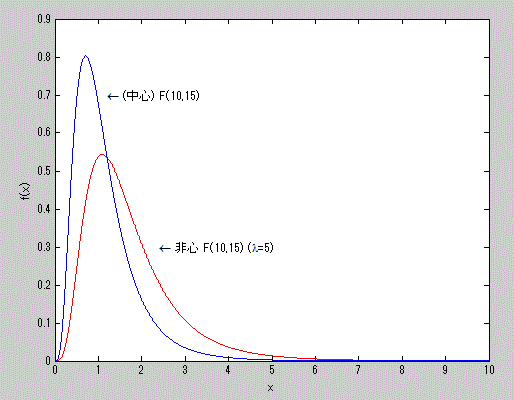
図14. (中心)F-分布と、非心度5の非心 F-分布の確率密度関数の比較
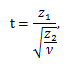
|
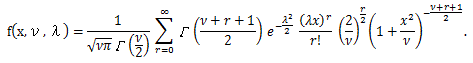
|
(101) |
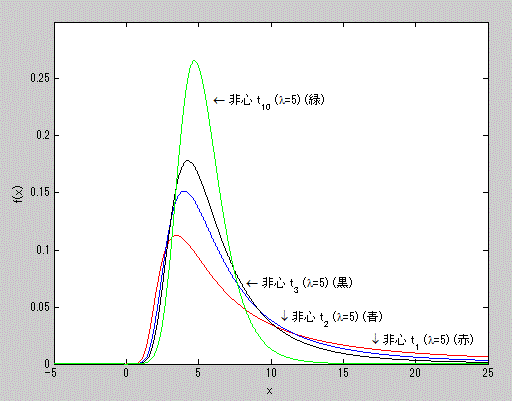
図15. 非心度5の非心 t-分布の確率密度関数の例
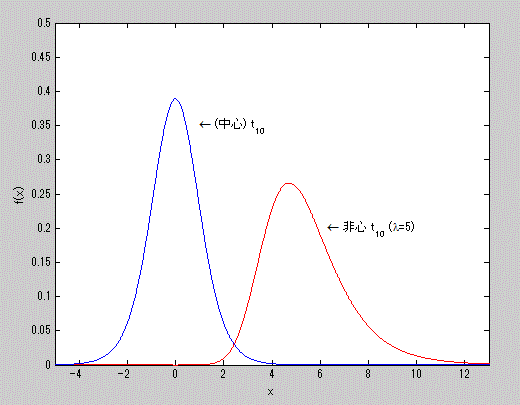
図16. 自由度10の(中心)t-分布と、同非心度5の非心 t-分布の確率密度関数の比較
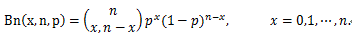
|
(102) |
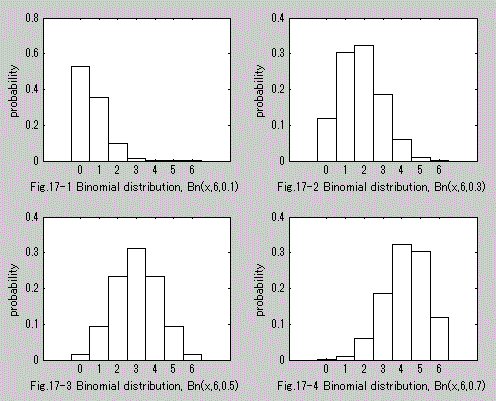
図17. 2項分布の確率関数の例
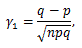
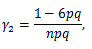
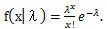
|
(103) |
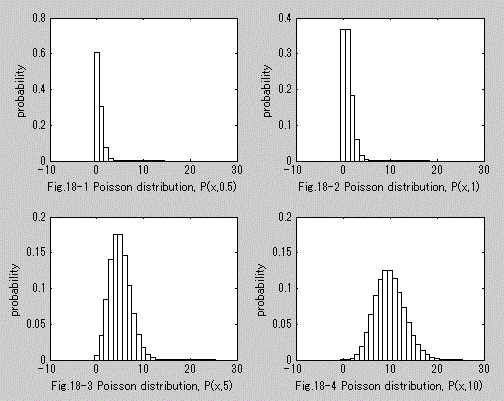
図18. Poisson 分布の確率関数の例
μ'1 = E (X)=λ、μ2 = V (X) = λ、μ3 = λ、μ4 = 3 λ2 + λ、γ1 = 1/(λ1/2), γ2 = 1/λ.
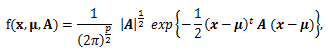
|
(104) |
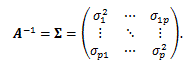
|
(105) |
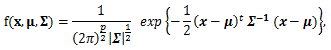
|
(106) |
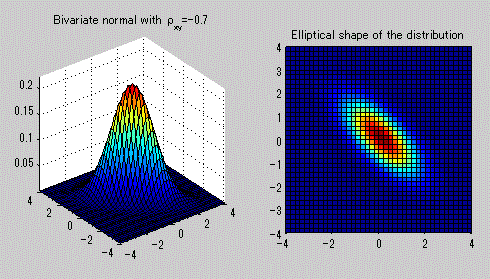
図19. 2変量正規分布の確率密度関数の例
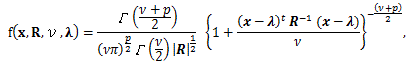
|
(107) |
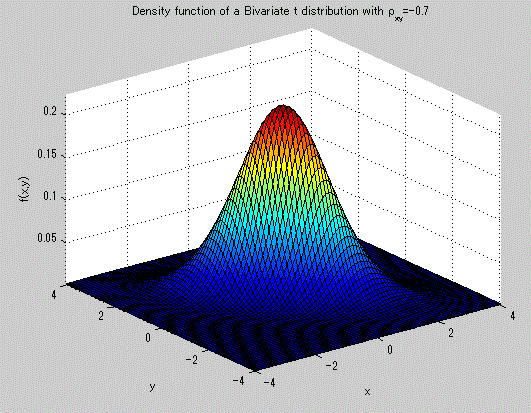
図20. 2変量 t-分布の確率密度関数の例
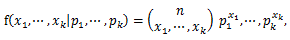
|
(108) |
 および
および
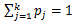 であるものとする。
さらに、右辺のカッコ記号は n 個の中にカテゴリー C1 が x1個、
カテゴリー C2 が x2個、...、カテゴリー Ck が
xk個含まれる組合せ (combination) 総数を表すものとする。ここで、各
xj (j=1,...,k) は、0 から n の値を取る。3.3.1 節の2項分布は、明らかに
多項分布の特別なケースである。
であるものとする。
さらに、右辺のカッコ記号は n 個の中にカテゴリー C1 が x1個、
カテゴリー C2 が x2個、...、カテゴリー Ck が
xk個含まれる組合せ (combination) 総数を表すものとする。ここで、各
xj (j=1,...,k) は、0 から n の値を取る。3.3.1 節の2項分布は、明らかに
多項分布の特別なケースである。
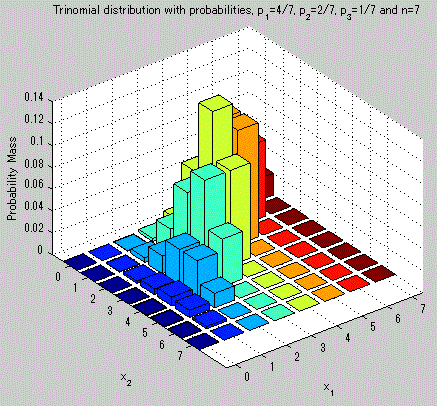
図21. 多項分布の確率関数の例(三項分布)
|
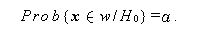
|
(110) |
これらの過誤を、それぞれ 第1種(Type I)の過誤 (error of the first kind)、
第2種(Type II)の過誤 (error of the second kind) と呼ぶ。
第1種の過誤は、 危険率 (level of significance) に等しい。第2種
の過誤を β と書くとして、1-β を 検出力 (power of the test) と
呼ぶ。統計的検定における帰無仮説は、多くの場合、何らかの母数間に差がないことを
意味するので、検出力が高い(1-β の値が大きい)検定とは、母数間に差が
ある時それを検出する力の大きい検定である、と言える。
一般に、帰無仮説の検定に際して同じ危険率を持つような棄却域のうち、いずれを
選ぶかという時には、第2種の過誤が最小、すなわち検出力が最大になるような
棄却域が望ましいと言える。このような棄却域は、 最良棄却域
(best critical region 略して BCR) と呼ばれる。また、BCR に基づく検定は
最強力検定 (most powerful test 略して MP 検定) と呼ばれる。
5.1 Bayes の定理
|
|
|
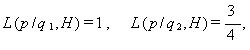
|
(113) |
|
|
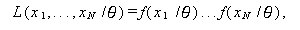
|
(114) |
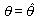 を選ぶのがよいことになる。
そのような
を選ぶのがよいことになる。
そのような 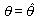 は、
最尤推定量 (maximum likelihood estimator) と呼ばれる。
は、
最尤推定量 (maximum likelihood estimator) と呼ばれる。
6.1 母数と推定量
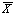 をここでは s と書くものとする。もちろん、
をここでは s と書くものとする。もちろん、
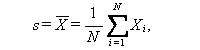
|
(115) |
であり、s は1つの統計量である。
さて、確率変数 X が平均 θ、で分散 σ2 に従うとすれば、 互いに独立なサイズ N の標本に対する確率変数の平均値 s は、
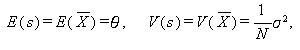
|
(116) |
なる正規分布に従うので、母平均 θ の 推定値 (estimate) として
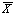 の実現値
の実現値
 を用いることは、1つの合理的な方法と言える。
ここで、一般に s のような統計量が推定のために用いられる時、これを
推定量 (estimator) と呼ぶ。また、一般に何らかの母数をうえのような
1つの値で推定する方法を、点推定 (point estimation) と呼ぶ。
を用いることは、1つの合理的な方法と言える。
ここで、一般に s のような統計量が推定のために用いられる時、これを
推定量 (estimator) と呼ぶ。また、一般に何らかの母数をうえのような
1つの値で推定する方法を、点推定 (point estimation) と呼ぶ。
これに対して、母数をある区間に入る確率の言葉で推定する方法を 区間
推定 (interval estimation) と呼ぶ。
うえの s=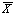 については、
については、

|
(117) |
が成り立つことを用いて、母平均 θ の信頼度 100(1-α) % の 信頼区間 (confidence interval) は、
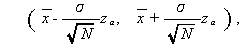
|
と書ける。ここで、zα は単位正規分布 N(0,1) の上側
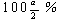 点を指す。
点を指す。
標本にもとづき母数 θ の推定を行う場合、θ の推定量が どのような性質を持つことが望ましいであろうか。これについては、従来から 数理統計学の分野では幾つかの特性が提案されてきた。1つは、推定量または その期待値と、その母数との一致・不一致に関する特性である。2つ目は、推定量 の 精度 (precision) とりわけ、推定量の ばらつき (dispersion) に 関するものである。3つ目は、推定量の持つ情報量に関するものである。4つ目は、 推定量の、母数からのばらつきに関するものである。
第1の性質には、 一致性 (consistency) と 不偏性 (unbiasedness) の2つがある。前者は、推定量の値が 漸近的に (symptotically) (すなわち サンプル数が無限大になった時に)母数 θ に一致するかどうか、という 性質である。これに対して、後者は、有限のサンプル数の場合、すなわち 正確に (exact) 推定量の期待値が母数に一致するかどうかという性質 である。
第2の性質についても、 最小分散 (minimum variance、略して MV) 性に、 2種類がある。1つは、推定量の漸近的な最小分散性で、他方は有限サンプル の場合のそれ(この場合には、さらに、MV の場合と 最小分散限界 (minimum variance bound、略して MVB) の場合がある)である。漸近的な MV は、古典的、有限サンプルの場合は近代的な意味での 有効性 (efficiency) の定義である。
第3の性質は、推定量の持つ情報の多さに関するもので、 充足性 とか 十分性 (sufficiency) と呼ばれる。
第4の性質は、推定量の、母数からのばらつきの小ささであり、 最小平均 平方誤差 (minimum mean-square-error) である。
|
もう1つは、 強い意味での一致性 (consistency in the strong sense) で、
|
いずれの場合も、一致性を持つ推定量は、 一致推定量 (consistent estimator) と呼ばれる。
例えば、(2.4) 節のチェビシェフの不等式を推定量  に対して
適用すると、
に対して
適用すると、
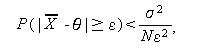
|
(120) |
が得られるので、N が無限大の時 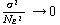 と
なり、したがって s =
と
なり、したがって s =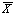 は母平均の一致推定量である。
は母平均の一致推定量である。
しかし、一般にある s が一致推定量であれば、例えば
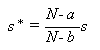
|
もまた一致推定量となる、すなわち一致推定量は一意的には定まらない。そこで、 有限のサンプル数に対して言及できる推定量の望ましい特性を考える必要性が 生じる。一般に、推定量 s の期待値が母数 θ に等しいとき、この推定量は 不偏性を持つといい、そのような推定量は、 不偏推定量 (unbiased estimator) と呼ばれる。正確には:
|
ならば、s は母数 θ の不偏推定量であるという。
推定量 s の精度は、しばしばその標本分散
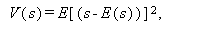
|
(122) |
で表される。推定量の多くは、中心極限定理により、漸近的には正規分布になる ので、n \to \infty$ の時、分布は平均と分散の2つの母数により決まる。 古典的には、漸近的に最小分散になるような推定量は、有効性があるといい、 そのような推定量を、 有効推定量 (efficient estimator) と呼ぶ。もっとも、 最近では漸近有効性も、1次、2次、3次等が区別されている。
いずれにせよ、古典的有効性が推定量の漸近的特性に関するものであるのに対して、 有限のサンプルの場合にも推定量 s の標本分散、すなわち精度に最小値が存在 することがわかったのは、比較的新しい。
Rao (1945) や Cram\'er (1946) により証明された クラメール・ラオの 不等式 (the Cram\'er-Rao inequality)
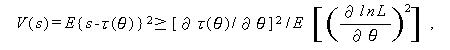
|
(123) |
は、推定量 s が母数 θ の関数 τ(θ) の不偏推定量である 場合に、推定量の最小分散限界 MVB を与える。
ここで、(123) 式の L は、互いに独立で同一な分布に従う (independent and identically distributed, 略して i.i.d. ) 母集団からの標本 x1, ... ,xN の尤度関数で、母数 θ のもとでの x1, ... ,xN の密度を f (x1 /θ), ... , f(xN / θ) と すれば、 5.4 節の (114) 式として表せる。また、τ(θ) は、推定 量 s の期待値すなわち、
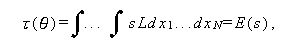
|
(124) |
である。
(123) 式は、 正則条件 (regularity conditions) と呼ばれるかなり 一般的な条件下で成り立つことがわかっている。この条件下では
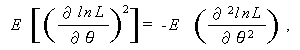
|
が成り立つので、(123) 式は
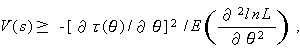
|
(125) |
とも書ける。
(125) 式の特別な場合は、τ(θ)=θ すなわち推定量 s が θ の不偏推定量の場合で、この時には、
|
が成り立つ。ここで、
|
は、標本における 情報量 (mount of information) と呼ばれる。この式から 明らかなように、推定量 s の最小分散限界は標本における情報量が増えると、 小さくなる。
MVB は、常に存在するとは限らないが、それより大きいところの最小分散 MV を持つ推定量は存在し、一意的に定まることがわかっている。この MV 推定量 (minimum variance estimator) は、近代的な意味での 有効推定量と言える。
正確には、
| 推定量 s は、母数 θ について、サンプルのすべての情報を含むとき、 充足性(十分性)がある、 |
という。また、そのような特性を持つ推定量は、 充足(十分)推定量 (sufficient estimator) と呼ばれる。
一般に、ある推定量が充足(十分)推定量であるかどうかの判定には、つぎの 分解基準 (factorization criterion) もしくは ネイマン基準 (the Neyman criterion) を用いる。
|
さて、母数 θ は θ=(θtr , θts)t な る列ベクトルとする。また、r \geq 1, s \geq 0$ であるとする。さらに、 5.4 節 で述べた標本の尤度関数を
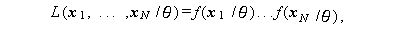
|
(129) |
とする。 5.4 節では、標本はベクトル量でなくスカラー量であったことに注意せよ。
この時、帰無仮説
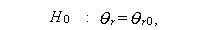
|
(130) |
を、対立仮説
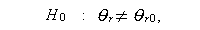
|
(131) |
に対して検定したいとする。うえの帰無仮説は、もし s =0 ならば単純仮説、 もし s \geq 1$ ならば、複合仮説である。
尤度比検定(likelihood ratio test) とは、一般につぎの尤度の比の 分布を用いて上述の帰無仮説を検定する方法である:
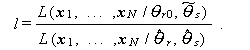
|
(132) |
ここで、分母は尤度
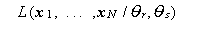
|
の無条件最大値を与える ML 推定量 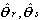 、
一方分子は (75) 式の帰無仮説が正しい時の尤度
、
一方分子は (75) 式の帰無仮説が正しい時の尤度
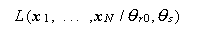
|
の、 θsの条件付き最大値を与える ML 推定量
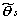 を
必要とする。
を
必要とする。
ただし、特定の場合を除き、一般的には尤度比の正確な分布はわかっていないので、
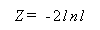
|
が帰無仮説のもとで、漸近的に自由度 r の χ2 -分布に従うことを利用し
て検定を行う。ここで、r は全母数 k =r + s から局外母数の数 s を差し引いた
ものである。
![]()