第1章 線形時系列解析と非線形時系列解析の違い
![]()
![]()
1.1 時系列解析の研究の歴史
| ||||
1.2 時系列データの例とそれらに対する解析結果
| ||||
1.3 時系列データの間引きの影響
| ||||
1.4 力学系の埋め込み定理
| ||||
| References |
この頁は、平成27(2015) 年2月15日に新たに開設しました。
この頁は、令和2(2020) 年8月9日に一部更新しました。
伝統的な時系列の解析は、Yule (1927) の自己回帰モデル (autoregressive model), 以下 AR と略す)に始まり、移動平均モ デル (moving average model, MA)、自己回帰移動平均モデ ル (autoregressive moving average model,ARMA) などのいわゆる 線形時系列解析よりなされてきた(例えば合原、2000)。また、同解析による時系列 信号の基本的な特性は、自己相関関数 (autocorrelation function)、 自己相関係数 (autocorrelation coefficient)、パワースペクトル (power spectrum) などを用いてなされてきた。
ここでは、1.1.1 節でまず最初に線形時系列解析の概要を紹介し、1.1.2 節で一般の時系列信号 の定常性 (stationarity) とエルゴード性 (ergodicity) について述べる。最後に 1.1.3 節で非線形 時系列解析とりわけカオス時系列解析の例を示す。
ここで、それらの表現のもとになるデータは2種類の T 時点の観測時系列信号であり、それらをy(t)、およびz(t)、t=1, .., T とする。 これらの信号は共に複数の要素からなり、順に s 個、m 個からなるベクトルである。
線形系 (lenear system) とりわけ線形時不変系 (linear time-invariant system) の第1の表現は、 系の入力ー出力表現 (the input-output representation) である。ここ では、離散時系 (discrete-time system) のみを扱い、時点は整数 (integers) Z上にまた がるか、場合により自然数(natural numbers) N上にまたがるものとする。
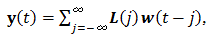
|
(1) |
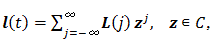
|
(2) |
ここで、(L(j) | j
Z) は (1) 式のウエイト関数 (weight function) と呼ばれる。ウエイト関数は、
y (t)=L(t-τ) e (τ) が時点 τでのインパルス、e (τ)、から生じる
出力の時間履歴であるので、インパルス応答関数 (impulse response function)、とも呼ばれる。
2つ目の系の表現は、ベクトル差分方程式表現 (the vector difference equation (VDE) representation) である。
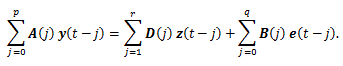
|
(3) |
ここで、y (t), z (t) およびe (t) は順に、出力、(観測)入力、および
誤差であり、A (j)
Rs×s、D (j)
Rs×m、および B (j)
Rs×s なるパラメータ行列である。
(3) 式のベクトル差分方程式表現で、さらに e (t) がホワイトノイズ (white noise) であり
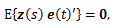
|
(4) |
であるならば、外生変数を伴う自己回帰移動平均系あるいはモデル) ARMAX (autoregressive-moving average system with exogeneous variables) と呼ばれる。
もし、(3) 式で外生変数が存在しないときは
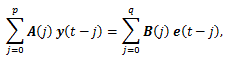
|
(5) |
自己回帰移動平均系 (the autoregressive-moving average system) または 1.1 節の冒頭で述べた自己回帰移動平均モデル ARMA と 呼ばれる。さらに、(5) 式はその特別な場合として、もし q=0 ならば自己回帰系 (autoregressive system) あるいは自己回帰モデルと、またもし p=0 ならば 移動平均系 (moving average system) あるいは移動 平均モデルと呼ばれる。
3つ目の系の表現は、状態空間表現 (the state-space representation)
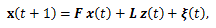
|
(6) |
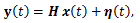
|
(7) |
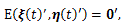
|
(8) |
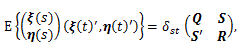
|
(9) |
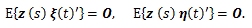
|
(10) |
(6)、(7) 式で表される系の状態空間表現、とりわけ、(6) 式は、(2) 線形系のベクトル 差分方程式表現と同様、差分力学系と見れるが、式の形は前者より単純な形をしている。すな わち、(6) 式はこのサイトの付録「心理学における力学系の理論と方法」の第2章 2.1.2 節の (2.7) 式で示した 線形一次差分方程式系 の右辺に観測入力 z (t) と誤差 ξ (t) に関する項が加わったものと見れる。いずれにせよ、系の状態空間表現は Kalman (1960) による工学の分野における制御理論 (control theory) をその基 礎に置くものであり、(6) 式の右辺第2項は系の制御 (control) にあたる。
上記 (6)、(7) 式で表される系の状態空間表現は、計量心理学の領域で開発されてきた多変量 解析の1つの方法としての SEM の表現
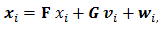
|
(11) |
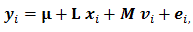
|
(12) |
両解析のもう1つの大きな違いは、Molenaar (2003) が指摘しているように、
最後に、線形力学系の状態空間表現である (6)、(7) 式は、つぎの形の状態空間系 (the state-space system) として表現できる。
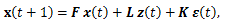
|
(13) |

|
(14) |
一般に時系列解析では、解析の前提として時系列信号の定常性 (stationarity) を仮定することがしばしばある。実際、例えば前節で述べた ARMA モデルを現実の時系列信号に 当てはめると、定常性を持つ時系列に対する適合度はよいことが知られている(例えば、 Hannnan, 1970)。
この節では前節と異なり、簡単のためにそのような時系列信号は1次元であるとし、それを f (t) と書くことにする。時系列信号が定常時系列 (stationary time series) であるとは、 f (t) の平均 (mean, or average) も自己相関関数 (autocorrelation function) も時間に関わ らず一定であるものを言う。 なお、定常性につい ては、より正確には、弱い定常性と強い定常性を区別することが必要である(例えば、日野、 1977, 2013)。まず、弱い定常性 (weakly stationary)とは、時 系列信号 f (t) が、平均μ一定で、かつ自己相関関数 C(t1, τ) がタイムラグτに のみ依存する関数であるときを指す。ここで、
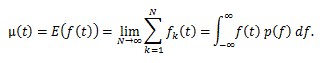
|
(15) |
一方、自己相関関数は、つぎのように定義される。
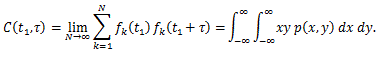
|
(16) |
上記の平均と自己相関関数を用いて弱い定常性を定義するとつぎのようである。
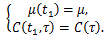
|
(17) |
一方、自己相関関数がすべての高次のモーメント まで時間にかかわらず一定のとき、時系列信号は強い意味で定常 (strongly stationary or stationary in the strict sense) といわれる。また、弱い定常性 も強い定常性も持たない時系列信号は、非定常 (nonstationary) といわれる。例えば株価変動や地震波などは典型的な非定常信号の例である。非定常信号に対す る対処方法にはこれまでいろいろなモデルが提案されているが、その1つは、時点間の信号の 差分をとる方法であり、自己回帰統合移動平均モデル ARIMA (autoregressive integrated moving average model) と呼ばれる(なお、ARIMA の日本語 訳は現状では統計学関係の文献や辞典でもなぜかほとんどなされていない)。
最後に、時系列信号が定常的であり、任意のサンプル k についての時間平均 μ (k)、C (τ, k)、 すなわち
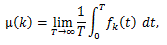
|
(18) |
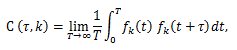
|
(19) |
がサンプル k によらず、アンサンブル平均 μ及び C (τ) に一致する時、すなわち、
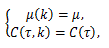
|
(20) |
の時、エルゴ―ド性 (ergodicity) を持つ、と言われる。
定常的ではあってもエルゴード性がないつぎのような不規則変動もある(例えば、 日野、1977, 2013):
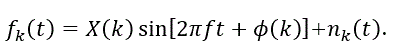
|
しかし、自然界から人間活動に至るまであまねく観測される時系列信号には多様なもの があり、必ずしも前節で紹介した線形時系列解析では把握しきれないことは明らかである。そこで、 近年ではこれに対して非線形時系列解析 (nonlinear time series analysis) に注目が集まっている。とりわけその中心は、カオス時系 列解析 (chaotic time series analysis)である。ここで、古くは古代バビロニア に遡るといわれ、Poincaré (1872) により基礎づけられたとされる(例えば、Schuster, 1988) 力学系の理論 (dynamical system theory) を基礎とする いわゆるカオス (chaos) は、 まず1960年代に気象現象に関する流体力学系 (hydrodynamical system) モデルにおいて Lorenz (1963) により報告され、1970年代には欧米の蝉 (cicada) の発生に関する生物学者 May (1976) により、1980 年代には心臓組織 (heart tissue) (Guevara et al., 1981)、 どろあわもち (Onchidium) の巨大神経 (giant neuron) (Hayashi et al., 1982)、脳活動 (brain activity) (Babloyantz, 1986)などで、1990年代以降では、プルキニェ繊維(Purkinje fibres) や心室筋 (Ventricular muscle) (Chialvo et al., 1990)、幼児の 泣き声 (newborn cries) (Mende et al., 1990)、ヤリイカの巨 大軸索 (squid giant axon) (Aihara et al., 1998; Mees, et al. ,1992)、 睡眠時・覚醒時脳波 (EEG in awake and sleep stages) (Pereda et al., 1998)、不規則声帯振動 (irregular vocal-fold vibration) (Titze, 1993)、指尖脈波 (pulse in finger capillary vessels) (Miao et al., 2006; Tsuda et al., 1992) 、脳波 (EEG)等 (Dafil's et al, 2013; Korn & Fauke, 2003) 、 鳥の鳴き声 (bird calls) (Fletcher, 2000)、 嗄声 (hoarseness) (Little et al., 2007)などでカオスが報告されている。
まず最初に、背後の系の振る舞いがわかっている場合の人工的時系列データを3つ示し、それら に対する伝統的(線形)時系列解析の方法としてよく知られている(スペクトル解析による)各 時系列信号のパワースペクトルと、非線形もしくはカオス時系列解析でよく用いられる各信号 の2次元空間への埋め込み、リアプノフ指数、及びリカレンスプロットの結果を示す。リカレンス プロットについては、その特性を強調するために、さらにエノン写像、周期時系列の1つである サインカーブ、いわゆる減衰振動時系列データ、及び一次元修正ベルヌイ写像の4つの時系列信 号も加えて、結果を示す。
つぎに、背後の系の振る舞いがわかっていない場合の観測時系列データを3つ示し、それらの 線形及びカオス(非線形)時系列解析の結果を示す。あとで述べるように、一般にどんな時系列 信号も定常時系列と非定常時系列の2つに分類することができるが、これら3つは共に後者の 非定常時系列信号である。
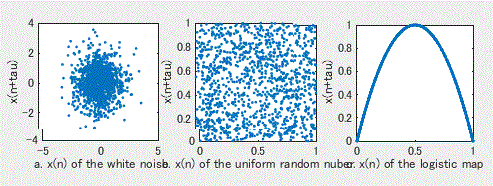
この節では、まず最初に伝統的な線形時系列解析では識別できない典型的な幾つかの人工的時系 列信号を示す。カオス時系列解析を用ればこれらの信号は明確に識別ができる。図1から3は、 Matlab を用いて生成した時系列信号をSunday Chaos Times(以降、SCT と略す)で出力したもの である。SCT は、「(株)あいはら」によるカオス時系列解析ソフトで、 SCTホームページから UNIX 版やWindows 版を入手できる。
ここで、ホワイトノイズ (white noise)は各時点で平均ゼロ、 分散1の正規分布に従うものを用いた。また、ロジスティック写像 (logistic map)
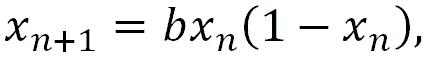
|
(21) |
は、別名ベリュルストーの力学 (Verhulst dynamics) とも呼ばれ、19世紀にベルギーの数学者ベリュルストーが提案したものである (Verhulst, 1838, 1845)。ちなみに、彼の名はこれまで本邦ではフェアフルストなどと呼ばれてきたが、筆者 は正確な発音はローマ字表現ではベリュルストーに近いことを、かつて彼が教鞭をとったベルギ ーの Ghent University の Kint, J. 教授に確認している。なお、ロジスティック写像について は、例えば、このサイトの第4章 2.1.4 節を参照のこと。また、より詳しい説明は例えば千 野(2008, pp.134-141)を参照のこと。
これらを見ると、3つの時系列信号は極めてランダムな振る舞いを示しており、3者共一見 不規則な信号のように見える。また、以下の解析結果から明らかなように、伝統的な時系列解析、例えばスペクトル解析 (spectrum or spectral analysis) の1つであるパワースペクトル密度 (power spectrum density) をみると、これらのスペクトルは周波数領域に関して(小さな周波数領域を除くと)すべてフラッ トで識別できないことがわかる。

しかし、これらのカオス時系列解析、例えばこれらの1次元信号 の2次元空間への埋め込み (embedding) を行ってみると、以下に 見るように、明らかに最初の2つの信号はでたらめな振る舞いを見せているが、最後のロジス ティック写像だけはでたらめではなく一種の規則的な振る舞いを示していることがわかる。
また、上記ソフト SCT を用いてカオス時系列解析の定番である リアプノフ指数 (Lyapunov exponents, あるいは Lyapunov characteristic numbers) を計算 すると、図6、7、8のようになる。両者は計算時の近傍数を20 と 小さく取った場合のものである。これだけをみると、最大リアプノフ指数はホワイトノイズ時系列データと一様乱数 時系列データの場合は小さいが正、ロジスティック写像の場合は相対的には大きめの値に収束していることがわかる。
しかし、計算時の近傍数を徐々に大きくとって最大リアプノフ指数の変化を見る、すなわち それらの局所対大域プロット(local versus global plots(例えば、 Ikeguchi & Aihara, 1997; 合原編、2000, pp.179-185) を行ってみると、ホワイトノイズ 時系列データと一様乱数時系列データのの場合には最大リアプノフ指数は負になるのに対して、 ロジスティック写像の場合正となり、ロジスティック写像時系列データのみがカオスの特性を 持つことが確認できる。もっとも、最後のロジスティック写像の場合、理論的な最大リア プノフ指数は ln 2、すなわち、およそ 0.693476 である(例えば、Sprott, 2003) が、3次元 空間に埋め込んだ場合のそれは、局所対大域プロットにより近傍数を大きくしていった場合 必ずしもこの近くの値に収束したとは判定できない。
もっとも、ロジスティック写像の場合は、1次元写像であるので、埋め込みパラメータの1つ である埋め込み次元を1としてリアプノフ指数を推定すると、近傍数 20 から 200 までの値は 落ち着いており、平均が 約 0.6934755 となり、理論通りの値が得られる。
このような結果は、リアプノフ指数の推定に際して埋め込みパラメータ (embedding parameters) (Kennel et al., 1992)(すなわち、埋め込み次元数とタイムラグの大きさ) の適切な推定が如何に大切かを示唆している。
もっとも、伝統的な線形時系列解析の場合もカオス時系列解析の場合も、それぞれの指標の 計算には大きな前提がある。まず線形時系列解析の場合、図1から3のような時系列信号は、 定常時系列であるという前提が置かれている。
一方、カオス時系列解析で例えばリアプノフ指数を計算する前提は、当該時系列が エルゴ―ド的である(例えば、Oseledec, 1968; Sano & Sawada, 1985)、というものである。
ただし、1.1.2 節でのべたように、うえの意味での時系列信号の定常性は、正確には弱い 意味での定常である。一方、自己相関関数がすべての高次のモーメントまで時間にかかわらず 一定のとき、時系列信号は強い意味で定常といわれる。また、弱い定常性も強い定常性も持 たない時系列信号は、非定常といわれる。
これらの前提を必要とせず、時系列信号の多様な性質を描き出すことが可能な方法として、 近年リカレンスプロット(recurrence plots, 略してRP)が注目 されている。RP は、Eckmann et al. (1987) が提唱したもので、1990年代以降多くの研 究がなされている(例えば、Casdagli, 1997; 大ら、2002; Fletcher, 2000; 平田、2011; Hirata & Aihara, 2010; 寶来ら、2002, 2014; Ikeguchi et al., 1996; Ngamga et al., 2008; Romano et al., 2004; Zbilut et al., 1998; 山田・合原、1999; Zbilut & Webber, 1992)。
例えば、上記ホワイトノイズ、一様乱数、及びロジスティック写像のリカレンスプロット のカラー画像を示したものが図9から11である。ちなみに、カラー表示は平面上の度数の 違いをカラーグラデュエーションで表すものである。なお、これらの図では、左上三角部と 右下三角部で色が異なるが、前者は後者のデータの対数を取ったものである。
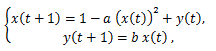
|
(22) |
で a=1.4、b=0.3 の場合の x-軸座標の時系列を図 12 に示す:
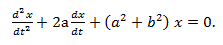
|
(23) |
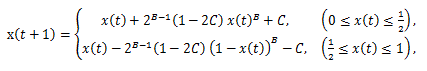
|
(24) |
を表す (24) 式のパラメータのうち、B=3、C=0 としたケースである。また、写像の初期値は x (1)=0.1 と した、この修正ベルヌイ写像時系列信号の特徴は、図にあるように激しく振動 するバースト層 (the bursting phase) と振動のないラミ ナー層 (the laminar phase) から成る点である。なお、彼らによれば、(24) 式のパラメータのうち C がゼロでない小さな値をとる場合には、この時系列はある限られた領域で定常的な時系列となり、f-ν スペクトル (the f-νspectrum) が観測できるという。
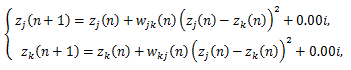
|
(25) |
による人工的データである。ここで、当初 Chino (2000, 2002) では、zj (n) と zk (n) は、一般的には(有限次元)複素ヒルベルト空間上で の対象 j および k の第 n 時点での位置座標を、wjk (n) は対象 j から対象 k への第 n 時点での重み係数で実数値をとり、右辺最後の項の i は純虚数を表し.(次式で定義される)重み係数
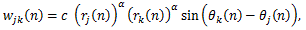
|
(26) |
は実数値をとるものと仮定していた。ここで、(26) 式の右辺の rj (n) および rk (n) は、対象 j および k の複素ヒルベルト空間上での原点からの長さを、 θj (n) および θk (n) はそれらの対象の偏角、すなわち各対象の 実軸からの半時計周りの角度(ラジアン)を表す。また、c および α は実定数であり、ここでは ともに 1/50 とした。(26) 式の性質から wkj (n)=-wkj (n) は自明で ある。

|
(27) |
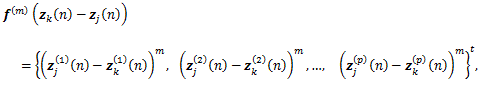
|
(28) |
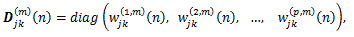
|
(29) |
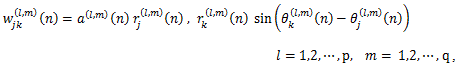
|
(30) |
の特別なケースであることに注意されたい。ここで、(27) 式の N は対象数であり、(25) 式では N=2 であることに注意したい。また、(27) 式の zj (n) は、対象 j の p-次元(複素) ヒルベルト空間あるいは p-次元不定計量空間 (indefinite metric space) における位置座標ベクトル である。さらに q は同差分方程式の最大次数である。
したがって、(27) 式から(30) 式で表される一般モデルにおける関係は2者関係に限定されず、 N の指定次第では3者以上のモデルも含むことがわかる。 また、最近Chino (2014, 2015) は、(26) 式の rj (n) および θj (n) が z とその共役複素数の関数になっているため、(25) 式やその一般化したモデル (27) 式が複素空間上の 正則関数 (holomorphic function) にならない点を指摘し、数学の分野 で開発されてきた複素力学系(例えば、上田ら、 1995)の知見を使え ないことを踏まえ、それに対処するための方法を考察している。
具体的には、1つの方法は、上記のモデルを特別ケースとして含むモデルには (p-次元)複素ヒルベルト空間を仮定せず、2p-次元のユークリッド空間 (Euclidean space) と同一視することであり、この種のモデルを族1モ デル (family F1)と呼んでいる。このように考えれば、上記モデルを無理なく定義できる。 ただし、その場合、複素力学系の理論を援用することはできない。
2つ目の方法は、族1モデルにおける (26) 式の仮定を取り除くモデルを考えることであり、 Chino (2015) はそのようなモデルを、族2モデル (family F2) と呼ぶ。 族2では、われわれはモデルの考察に複素力学系の知見を使うことが可能である。3つ目の 方法は、族2のモデルの右辺に制御項や複素定数(実定数も可)を加えるもので、Chino (2015) は それを族3モデル (family F3)と呼ぶ。
まず、図 24 から図 2図24 から 図26 は、最初から1万個、3つ目の一万個、5つ目の一万個 の時系列信号を示す。
図 37. の時系列信号の中から最初の一万回、3つ目の一万回、5つ目の一万回の信号を取り 出して描いたのが、図 38、図 39、図 40 である。

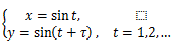
|
(31) |
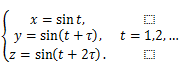
|
(32) |
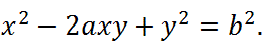
|
(33) |
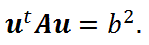
|
(34) |
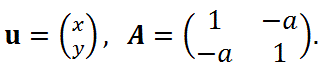
|
(35) |
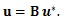
|
(36) |
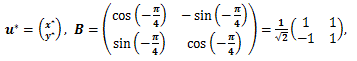
|
(37) |
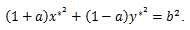
|
(38) |
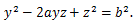
|
(39) |
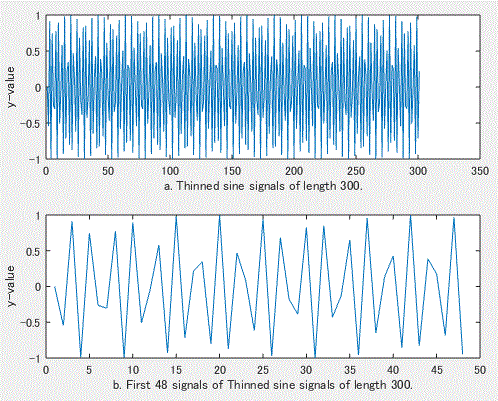
図 47. 正弦波の 1/100 間引き後の信号とその一部切り出し

図 48. 正弦波の 1/100 間引き後の信号の3次元埋め込み結果(点列の隣接2時点間を線分で 結んだもの)
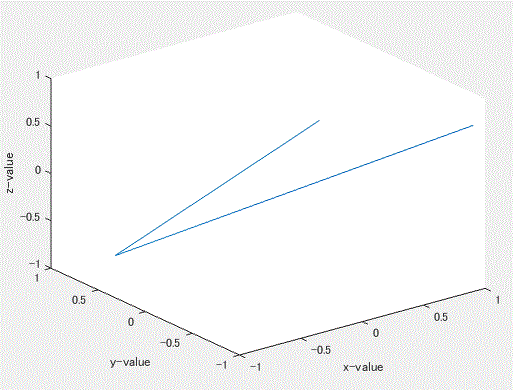
図 49. 正弦波の 1/100 間引き後の信号の3時点分の3次元埋め込み結果(点列の隣接2時点間を線分で 結んだもの)
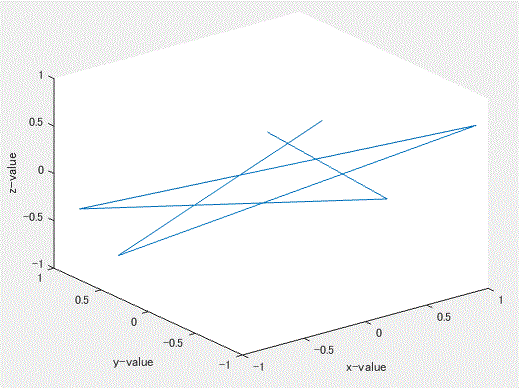
図 50. 正弦波の 1/100 間引き後の信号の6時点分の3次元埋め込み結果(点列の隣接2時点間を線分で 結んだもの)
なお、(株)あいはらの SCT (Sunday Chaos Times) でも解軌道の多次元空間への埋込みに際し ては、うえのような例の場合にも隣接2時点間を線分で結ぶので注意が必要である。
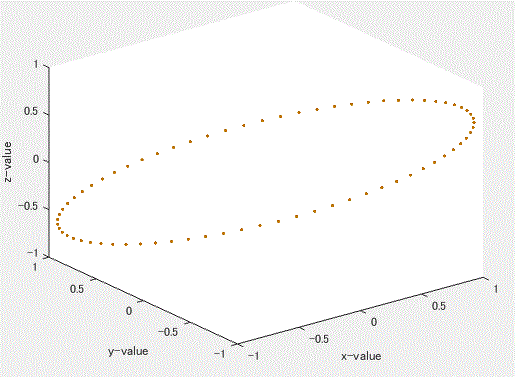
図 51. 正弦波の 1/100 間引き後の信号の3次元埋め込み結果(点列のみ)
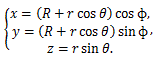
|
(40) |
図 52. 幾何学的トーラス(輪環面)の3次元表示
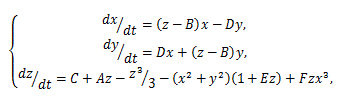
|
(41) |
なる3次元の非線形1階微分方程式系であり、よく知れているようにパラメータ A、B、 C、D、E、F によりトーラスやカオスが得られる。図53は、2-トーラス(準周期解)を 生成する A=1、B=0.7、C=0.6、D=3.5、E=0.25、F=0 の第1変数の解軌道 を示す。また、図 54はこの第1変数の解軌道を3次元空間に埋め込み、隣接2時点間を 線分で結んだものである。これに対して、図 55 は3変数の解軌道を3次元上に点列とし て表示したものである。
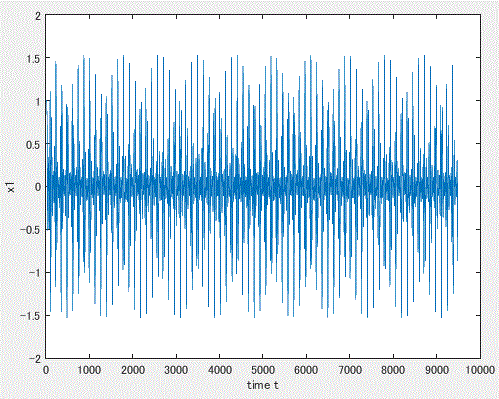
図 53. ラングフォード方程式の第1変数の時系列信号
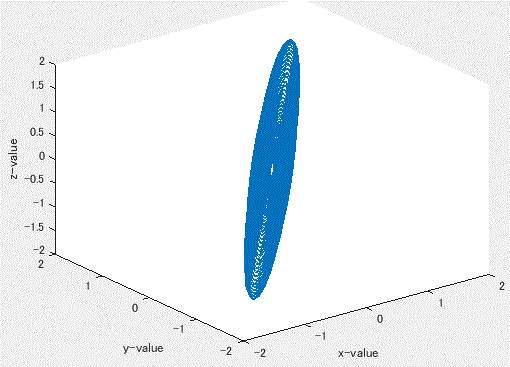
図 54. ラングフォード方程式の第1変数の解軌道の3次元埋め込み結果(点列の隣接2時点 間を線分で結んだもの)

図 55. ラングフォード方程式の解軌道のトーラス局面(点列)
さらに、周期的信号が単純な正弦波のようなものではなく、複数の周期の波が周期的に繰 り返すような信号の場合はどうであろうか。そのような場合、間引き間隔次第では特定の周期 の波がすべてカットされてしまうケースがあるとすれば、間引き前と間引き後で信号の位相 は異なったものにならないであろうか。一方、間引き間隔を等間隔に取らないでランダムに取った 場合 (nonuniform sampling) は、どのような位相になるか予想できない。また、カオス力学 系の信号を等間隔で間引くと同相な信号が予想されるが、ランダムに取った場合はどんな位相 になるのであろうか。
この問題に対して、歴史的にはこれまで少なくとも2つの研究の流れが ある。1つは、古くから知られたナイキストーシャノンの標本化定理 (Nyquist-Shannon sampling theorem) (例えば、Mishali et al., 2009; Nyquist, 1928; Shannon, 1949) に関係するもので、工学における信号検出の問題と見れる。他方は、いわゆる 力学系の埋め込み定理 (embedding theorems) (例えば、Sauer et al., 1991; Takens, Takens, 1981; Whitney, 1936) に関わるもので、数学における 可微分多様体 (differentiable manifold) の理論を背景に持つ 問題である。次節では、後者の埋め込み定理について述べる。
実は、Whitney (1936) に始まる埋め込み定理の展開の歴史をたどると、上記の問題につい ては既に幾つかの結論が出ていることがわかる。とりわけ、上記最初の問題やつぎの複数の 周期の波が周期的に繰り返すような信号の場合には、以降に紹介した定理のうち 1.4.2 節 の観測1次元時系列の遅延埋め込み定理の中の Sauer et al. (1991) の Theorem 2.5 の中 で解答が得られていることがわかる。例えば、正弦波時系列に限らず一般の周期時系列を含む ような時系列においては、当該周期時系列の周期と一致する間引き間隔で間引くと、もとの 時系列の位相は円であるが、間引かれた時系列の位相は線になってしまい、位相が異なるもの になる。千野 (2015) は正弦波時系列の間引きに関するシミュレーションを行っているが、 そこでは、間引きが等間隔の場合、如何なる間隔でサンプリングしてもその位相は円になる、 と結論づけれているが、間隔が時系列の周期と一致する場合はこれに該当しないことを見落 としていた。
|
すなわち
|
なお、文献上では、Whitney の上記埋め込み定理を若干修正したり簡素化した定理として紹介 しているものが見られる。例えば、Sauer et al. (1991, p.583) は上記定理を Whitney の 埋め込み生成定理 (the embedding genericity theorem of Whitney (1936) としてつぎのように表現している。ここで、Sauer et al. は R をユーク リッド空間の意味で使っていることに注意したい:
|
うえの定理で、Sauer et al. は、「生成的(generic)註9」 という概念を C1-位相における開で稠密な (open and dense) 集合 註4という意味で使っている。いずれにせよ、 合原編(2000, p.17) の定理 2.2.1 (ホイットニーの埋め込み定理)は、以下のように記 されているが、明らかに上記 Sauer et al. の表現を踏襲している:
|
一方、Guillemin and Pollack (1974, p.53) はもとの Whitney (1936) の定理 を Whitney 定理(Whitney theorem)として次のように簡単に表現 している:
|
Whitney (1936) は上記の埋め込み定理のみでなく、幾つかの他の定理についても述べている。 そのうちの1つは Theorem 3(p.655) である。なお、これは彼の原著の Theorem 2 (p.654) に も関係する:
|
この定理では、彼の上記 Theorem 1 と比べて、埋込みの次元が1つ減っていることに注 意したい。ただし、この場合、埋め込み先の多様体は regular註13 という制約がついている。このような写像は、正確には埋め込み(embedding) ではなく、 はめ込み (immersion) 註14 と呼ばれる。Guillemin and Pollack (1974, p.55) は、この定理を簡略化してつぎのように表現 している:
|
Sauer et al. (1991) は、 Whitney の埋め込み定理をプレバレンス 註15 (prevalence) なる概念を導入することにより、 つぎのような定理として拡張した。なお、ここでも彼らは R をユークリッド空間の意味で 用いていることに注意したい。また彼らはなめらかな写像 (smooth map) を C1級 の意味で用いていることにも注意したい:
|
うえの定理を合原編 (2000, p19) では、定理 2.2.2 として以下のように表現している:
|
Sauer et al. (1991) は、うえの theorem 2.2 で A が多様体でない場合にも拡張した。つぎの 定理はそれを示す:
|
ここで、ボックスカウント次元 (box-counting dimension) とは、 一般に任意の図形の次元のうち、 非整数値をとる場合の1つの指標である。通常の図形、例えば線、平面、立体は順に1次元、2次元、 3次元の図形であるが、特別な図形ではこの値が整数ではなく、非整数値を取るものがある。例えば、 コッホ曲線ではボックスカウント次元は 1.26... である。
この定理における完備な多様体 (compact manifold) 上の力学系は、 離散時間 (discrete time) の場合微分同相写像 (a diffeomorphism) φ: M → M、連続時間 (continuous time) の場合 M 上のベクトル場 (vector field) とする:
|
ここで、Takens は「なめらかな」(smooth) という意味を、”少なくとも C2級”の
意味で使っているが、Noakes (1991) は、C1級を含めて Ck級
(k1) としている。なお、
上記の時間遅れ座標系に関しては、Sauer et al. (1991, p.588) は、遅延座標写像
(delay-coordinate map) という表現を使い、以下のように定義している:
|
ここで、遅延座標写像を得るということは、1次元の時系列データ h(x) から一定の時間間隔 T ごとにデータ をサンプリングすることを意味する。また、そのようにして得られた数値は時系列 (time series) とみなされ る。もちろん、T を上記定義のように T, -2T, …, -(n-1)T のような下降系列として定義しても、 T, 2T, …, (n-1)T のように上昇系列として定義しても、本質的には何らかわりはない。
なお、合原編 (2000, p.23) では、上記 Takens の定理をつぎのように表現している。以下の 定理では、Takens (1981) でのパラメータ m を d と表現しており、また埋め込 み次元を m>2d と不等式を用いて表現している:
|
Sauer et al. (1991, p.590) は、上記 Takens (1981) における、(1)「次元 d のなめらか な多様体 (smooth manifolds)」を「ボックスカウント次元 d を持つ完備集合 (compact sets) 」に、また(2)「生成的 (generic)」を「プレバレント (prevalent)」に置き換えることにより拡張した。つぎの Theorem 2.5 は、これを示す:
|
ここで、上記 Theorem 2.5 での遅延座標写像 F (h, φ, T) は、Sauer et al. (1991) の少し上で紹介 した Definition 2.4 のそれである。また、流れ (flow) とは連続時間上の 微分方程式の解軌道を指すので、上記定理は連続系の場合の定理と言える。 また、Sauer et al. (1991) は同論文の中のなめらかな関数 (smooth function) を C1 級 の意味で使っていることに注意されたい。なお、上記定理の中の軌道の「線形化 (linearization)」については、このサイトの「付録 心理学における力学系の理論と方法」の中の 1.1.3 節 非線形一次微分方程式系の項を参照されたい。
Sauer et al. (1991) の上記 Theorem 2.5 からは、d 次元のボックスカウント次元を持つ k 次元ユークリッド空間 Rk の開集合 U から n>2d 次元ユークリッド空間への遅延 座標写像は、φを U 上の流れ (flow) とするとき、U 上の完備な開集合 A が
このように、Sauer et al. (1991) の Theorem 2.5 では、上記 Theorem 2.2 や Theorem 2.3 の場合と異な り、遅延座標写像が埋込みであるためには幾つかの特別な条件が必要であることがわかる。とりわけ、それら の条件のうち、2. と 3. はφの周期軌道に関するもので、周期が T または 2T になるような周期軌道の存在のみを否定している点が興味深い。その理由を Sauer et al. (1991, p.589) は、つぎのように説明している:
まず、A が連続力学系の周期軌道で、その周期がサンプリング区間 T に等しい場合、 位相的には A は円 (circle) である。この場合、遅延座標写像 F (h, φ, T) は如何なる観測 関数 h に対しても1対1 (one-to-one) にはならない。なぜならば、A の周期は T なので、h(x)=h(φ-T(x))= … =h(φ-(n-1)T(x)) となり、写像 F (h, φ, T) は、点 x を R n 上の対角線 (diagonal line) {(x1, … , xn): x1= … = xn} に写像する。円は連続的には線 (line) には 1対1では写像できない。
1対1写像は、A が周期 2T の周期軌道の場合も成り立たない。ここで、A 上の関数 d(x)=h(x) - h(φ-T(x)) を定義する。関数 d は A 上のいずれかの 点 x に対して恒等的にゼロまたは非ゼロであり、その場合それは写像点 φ-T(x) で 逆符号を持ち、A 上で符号を変える。いずれにせよ、d(x) は A 上で根 x0 を持つ。A の周期は 2T なので、h(x0)=h(φ-T(x0))= h(φ-2T(x0))= …. そこで、F (h, φ, T) は x0 と φ-T(x0) を R n 上の同一点上に写像する。もし、x0 と φ-T(x0) が相異なる場合には、このことは F が1対1ではないことを 意味する。これに対してもし x0 = φ-T(x0) であれば、軌道は実際 周期 T を持ち、F は上と同様1対1ではない。すなわち、周期 2T なる軌道の出現 により、、F (h, φ, T) は如何なる観測関数 h に対しても1対1では有り得ない。
合原編 (2000, p.24) の以下の定理 2.2.5 は、上記 Theorem 2.5 を遅延座標を補足して訳したものである。なお、合原編では、「遅延」を「時間遅れ」と記している:
|
ここで、上記 Sauer et al. (1991) の Theorem 2.5 に戻ると、この定理はつぎに示す微分 同相写像 (diffeomorphism) の特別な場合である。
|
ここで、Sauer et al. (1991) の少しうえの Definition 2.4 では h は なめらかな関数 (a smooth function) であるが、Definition 2.6 では h は単に 関数 (a function) となっていることに注意したい。いずれにせよ、 Definition 2.6 の関数を仮定すると、Theorem 2.5 におけるφを g と置き換える、す なわち Theorem 2.5 において g =φ-T とすれば、Sauer et al. (1991) に よるつぎの定理が得られる:
|
上記定理は Theorem 2.5 とは対照的に、離散系の場合の定理と言える。 合原編 (2000, p.24) の定理 2.2.6 は、この定理に若干補足して訳したものである:
|
(註1)Cr級とは、
一般に関数が r 回微分可能であることをいう。
(註2)一般に n 次元多様体 M、n-多様体 (n-manifold) 、ある
いは n 次元位相多様体 (n-dimensional topological manifold) とは、
1つの位相空間 (topological space) で、つぎの性質を持
つものをいう: (1) M はハウスドルフ
(Hausdorff) である。(2) M は局所的に(locall) n 次元ユークリッド空間(En)であ
る。 (3) M は下位集合の加算基 (countable basis) を持つ(例えば、Boothby, 1975, p.6;
数学辞典、2008)。
(註3)なお、位相空間は任意の相異なる2点が互いに素な近傍 (neighborhoods) を持つ時
ハウスドルフと呼ばれる。また、位相空間は一般に距離の概念を導
入することなく集合論の観点からつぎのように定義される。すなわち、位相
空間とは集合 X とその下位集合の集合 Q からなる対 (X, Q) でつぎの性質を持つもの
である: (1) 開集合の和集合が開集合である。(2) 2つの開集合の共通集合が開集合である。
(3) 空集合φとX が開集合である(例えば、Janich, 1984, p.5)。
(註4)位相空間 (X, Q) において、開集合の補集合を X の
閉集合
(closed set) という。X の任意の部分集合 A に対して、A を含む X の閉集合全体の共通集合
は X の閉集合であり、これを位相空間 X における A の閉包 (closure)
という。また、A の閉包が X に等しいとき、A は X で稠密
(dense) であるという(同上、数学辞典)。
(註5)M を n 次元位相多様体とし、M の下位集合 U と U からユークリッド空間 En
の開集合への同相写像φとの組 (U, φ)を M の座標近傍
(coordinate neighborhood) という。En の点 φ(p) (pU) のEnにおける座標を (x1
(p), …, xn(p)) とすれば、x1, …, xn は U 上の実数値
関数であり、これらの n 個の関数の組 (x1, …, xn) を座標近傍にお
ける M の局所座標系 (local coordinate system)、(x1(p),
…, xn(p)) を点 p の 局所座標 (local coordinate)
と呼ぶ。n 次元位相多様体 M の座標近傍の族 S={(Uα, φα)}
α
A
で {Uα}α
Aが M の開被覆 となるような
ものが存在する。このような S を M の座標近傍系 (system of
coordinate neighborhoods) と呼ぶ(同上、数学辞典)。
(註6)位相空間 X の部分集合族 M={Mλ}λA について、X=
λMλ であるとき、M を X の
被覆 (covering) という。さらに、被覆 M の元がすべて開集合である
とき、M を開被覆 (open covering) という(同上、数学辞典)。
(註7)n 次元位相多様体 M の座標近傍系を S={(Uα, φα)}
αA
とすると、S に属する任意の座標近傍 (Uα, φα)、 (Uβ,
φαβ) に対して、Uα
Uβ
φ ならば、φβoφα-1 は
Rn の開集合 φα (Uα
Uβ) から Rn の開集合
φβ
(Uα
Uβ) への同相写像である。Rn の座標 (x1, …,
xn) を用いて、(φβoφα-1) (x)=
(f 1βα(x1, …, xn), …,
f nβα(x1(xn,…, xn))と
いう形に表すことができる。n 個の関数 f 1βα, …,
f nβα が任意のα、β
A (ただし、Uα
Uβ
φ)に対して
r 回連続微分可能(または(実)解析的)であるとき、S を Cr
級座標近傍系 と呼ぶ(ただし 1
r
∞)(同上、数学辞典)。
(註8)n 次元位相多様体 M が Cr 級座標近傍系 S(ただし、
1r
ω)を持つとき、
M と S の組 (M, S)を n 次元 Cr 級微分可能多様体
(differentiable manifold of class Cr)、Cr
級多様体、またはCr 級可微分多様体と呼ぶ。
特にC∞多様体はなめらかな多様体 (smooth manifold) 、
また Cω多様体は解析的多様体 (analytic manifold)
とも呼ばれる
(同上、数学辞典)。
(註9)C∞ 写像の性質が(強い
意味で)生成的
(generic in the strict sense) とは、 Whitney の C∞ 位相での開かつ稠密な (open
and dense) 集合 U
C∞ (N, P) が存在して、U に属する任意の写像 f がその性質を持つことをいう。
(註10)X, Y を位相空間とし、X から Y への同相写像 (homeomorphism)
が存在するとき、X と Y とは同相、同位相または位相同型
(homeomorphic) という(同上、数学辞典)。
(註11)X, Y を位相空間とし、f を X から Y への写像とする。写像 f が
全単射 (bijection)で、f とその逆像 f-1 がともに
連続のとき、f を同相写像、または位相写像 (topological mapping)
という(同上、数学辞典)。
(註12)f (A)=B であるような写像 f:A→B を上への写像 (onto map)、または
全射 (surjection) という。また定義域が相異なる2つの元における値が常に異なる写像を
1対1写像(one-to-one) 、または単射
(injection) という。全射でもある単射は全単射 (bijection) という
(同上、数学辞典)。
(註13)写像は、もしそれぞれの点の近くで微分可能であり可微分
な逆像 (differentiable inverse) を持つとき、regular(正則)であ
るという(例えば、Whitney, 1936, p.645)。
(註14)写像φ: M → M' が C∞ 級写像のとき、M の
点での微分写像 dφ が単射(別名1対1)ならば、φはM の M' の中へのはめ込み
(immersion) という。一方、はめ込み写像φが単射のとき、φは M の M' の中への
埋め込み (embedding, or imbedding) という(同上、数学辞典)。
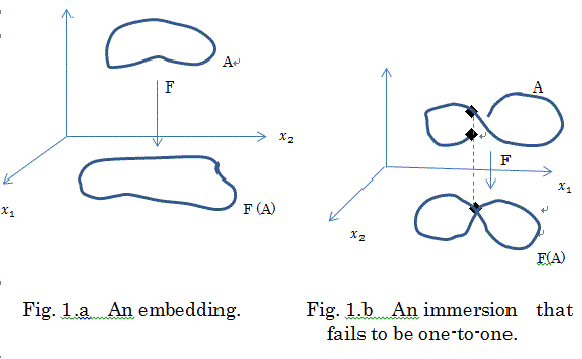
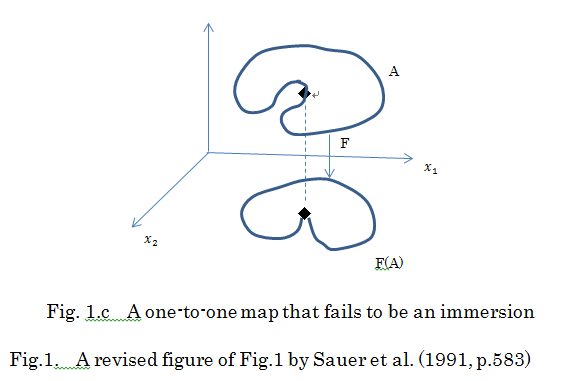
なお、Sauer et al. (1991, p.583) は、はめ込みと埋め込みの違いをわかりやすく次のように
図示している。ここで、図中相空間 Rk 上のすべての軌道は周期的サイクル (periodic
cycle) A に惹きつけられるとする。すなわち、A は位相的には Rk 上の
円である。ここで、2つの可能な測定量 Q1 と Q2 を平面上にプロットした
とする。このとき、A から R2 への F(状態)=(Q1, Q2)
により与えられる測定写像 F が存在する。問題は、隠れたアトラクター A の性質が
観測可能な"再構成空間" R2 上でどの程度保存されるかということである。
(註15)プレバレント (prevalent) とは、
任意のノルム空間 (normed linear space) における稠密性 (dense) を意味する(例えば、Sauer et al.,
1991)。
Aihara, K., Ikeguchi, T., Matsumoto, G. (1998). Deterministic nonlinear dynamics of a
forced oscillation experimentally observed with a squid giant axon. International
Journal of Chaos Theory and its Applications, 3, 5-20.
Aizawa, Y., & Kohyama, T. (1984). Asymtrotically non-stationary chaos. Progress
of Theoretical Physics,71,847-850.
Box, G. E. P. & Jenkins, G. M. (1970, 1976). Time series analysis: Forecastingand control.
San Francisco: Holden-Day.
Casdagli, M. C. (1997). Recurrence plots revisited. Physica D,108,
12-44.
Chialvo, D. R., Gilmour, R. F., Jr, & Jalife, J. (1990). Low dimensional chaos in
cardiac tissue. Nature, 343, 653-657.
Chino, N. (2002). Complex space models for the analysis of asymetry. In S. Nishisato,
Y. Baba, H. Bozdogan, & K. Kanefuji (Eds.) Measurement and Multivariate Analysis,
Tokyo: Springer. pp.107-114.
千野直仁 (2008). 集団のシステム解析ー微分・差分方程式モデルー 岡林春雄編著 心理学
におけるダイナミカルシステム理論 第7章 (pp.119-150). 金子書房
Chino, N. (2014). A Hilbert state space model for the formation and dissolution of
affinities among members in informal groups. Supplement of the paper presented
at the workshop on Problem Solving through the Applications of Mathematics to
Human Behaviors by the aid of The Ministry of Education, Culture, Sports, Science
and Technology in Japan, 1-24.
Chino, N. (2015). A simulation study of a Hilbert space model for changes in affinites
among members in informal groups. Journal of the Institute for Psychological and
Physical Science,7.
千野直仁 (2015). 正弦波時系列の
間引きによる解軌道の特徴について 研究ノート(力学系信号の間引きについての一考察)
Chino, N. & Shiraiwa, K. (1993). Geometrical structures of some non-distance models for
asymmetric MDS. Behaviormetrika, 20, 35-47.
Eckmann, J. -P., Olliffson Kamphorst, S., & Ruelle, D. (1987). Recurrence plots of
dynamical systems. Europhysics Letters,4,973-977.
Guillemin, V. & Pollack, A. (1974). Differential Topology, New Jersey: Prentice
Hall.
Guevara, M. R., Glass, L., & Shrier, A. (1981). Phase locking, period-doubling
bifurcations, and irregular dynamics in periodically stimulated cardiac cells.
Science, 214, 1350-1353.
Hamilton, J. D. (1994). Time series analysis. Princeton: Princeton University.
Hannan, E. J. (1988). The statistical theory of linear systems. New York: Wiley.
Hayashi, H., Ishizuka, S., Ohta, M., & Hirakawa, K. (1982). Physics Letters,
88A,435-438.
寶来俊介、山田泰司、合原一幸 (2002). 同方向リカレンスプロットによる決定論的解析
電学論 C,122, 141-147.
日野幹雄 (2013). スペクトル解析 新装版 朝倉書店
平田祥人 (2011). リカレンスプロット:時系列の視覚化を超えて 数理解析研究所講究録
1768, 150-162.
Ikeguchi, T., & Aihara, K. (1997). Lyapunov spectral analysis on random data.
International Journal of Bifurcation and Chaos, 7, 1267-1282.
Kalman, R. E. (1960). A new approach to linear filtering and prediction problems.
Transactions of the ASME-Journal of Basic Engineering, 82, 35-45.
Kennel, M. B., Brown, R., and Abarbanel, H. D. I. (1992). Determining embedding dimension
for pahse-space reconstruction using a geometrical construction. Physical Review
A, 45, 3403-3411.
Kohyama, T. (1984). Non-stationarity of chaotic motions in an area preserving mapping.
Progress of Theoretical Physics,71,1104-1107.
Lorenz, E. N. (1963). Deterministic nonperiodic flow. Journal of the Atmospheric
Sciences,20,130-141.
Manneville, P. (1980). Intermittency, self-similarity and 1/f spectrum in dissipative
dynamical systems. Journal de Physique,41,1235-1243.
Manneville, P., & Pomeau, Y. (1980). Different ways to turbulence in dissipative
dynamical systems. Physica D,1,219-226.
May, R. (1976). Simple mathematical models with very complicated dynamics. Nature,
261, 45-67.
Mees, A., Aihara, Adachi, M., Judd, K., Ikeguchi, t., & Matsumoto, G. (1992).
Deterministic prediction and chaos in squid axon response. Physical Letters,
A 169、41-45.
Miao, T., Shimoyama, O., Oyama-Higa, M. (2006). Modelling plethysmogram dynamics based on
baroreflex under higher cerebral influences. 2006 IEEE Conference on Systems, Man, and
Cybernetics, October, Taipei, Taiwan.
Mishali, M., & Edlar, Y. C. (2009). Blind multiband signal reconstruction: Compressed
sensing for analog signals. IEEE Transactions on Signal Processing, 57,
993-1009.
Molenaar, P. C. M. (2003). http://hhd.psu.edu/media/dsg/files/StateSpaceTechniques.pdf,
December 31, 2015.
Noakes, L. (1991). The Takens embedding theorem. International Journal of Bifurcation and
Chaos. 1, 867-872.
Nyquist, H. (1928). Certain topics in telegraph transmission. Transactions of the
American Institute of Electrical Engineers. 47, 617-644.
Oseledec, V. I. (1968). A multiplicative ergodic theorem. Ljapunov characteristic
numbers for dynamical systems. Transactions of the Moscow Mathematical Society,
19,197-231.
Sano, M. & Sawada, Y. (1985). Measurement of the Lyapunov spectrum from a chaotic time
series. Physical Review Letters,55,1082-1085.
Shannon, C. E. (1949). Communication in the presence of noise. Proceedings of the Institute
of Radio Engineers, 37, 10-21.
Schuster, H. G. (1988). Deterministic Chaos: an introduction. New York: Wiley.
Takens, F. (1981). Detecting strange attractors in turbulence. In D. A. Rand and B. S.
Young, (Eds.), Dynamical Systems of Turbulence, Vol. 898 of Lecture Notes in
Mathematics (pp.366-381). Berlin: Springer-Verlag.
Tsuda, T., Tahara, T., Iwanaga, I. (1992). Chaotic pulsation in capillary vessels and
its dependence on mental and physical conditions. International Journal of Bifurcation
and Chaos, 2, 313-324.
上田哲生・谷口雅彦・諸澤俊介 (1995). 複素力学系序説 培風館
山田泰司、合原一幸 (1999). リカレンスプロットと2点間距離分布における非定常時系列解析
電子情報通信学会論文誌、J82A, 1016-1028.
Yule, G. U. (1927). On a method of investigating periodicities in disturbed series, with
special reference to Wolfer's sunspot numbers. Philosophical Transactions of the
Royal Society of London, Series A,226,267-298.
Voss, R. F. & Clarke, J. (1977). '1/f noise' in music and speech. Nature, 258,
317-318.
Webber, C. L. Jr., Zbilut, J. P. (1994). Dynamical assessment of physiological systems
and states using recurrence plot strategies. Journal of Applied Physiology,
76,965-973.
Welch, P. D. (1967). The use of fast fourier transform for the estimation of power spectra:
A method based on time averaging over short, modified periodograms. IEEE transactions
on Audio and Electroacoustics,15,70-73.
References